Skip to contents

Sequential Design II

Source: vignettes/seq_design_2.Rmd
seq_design_2.Rmd

This vignette shows how to use the package to sequentially refine a bundle of DGP emulators, each of which emulates an output of a simulator.

Load the packages

Construct a synthetic simulator

We construct a synthetic simulator that has a one-dimensional input between [0, 1] and a three-dimensional output.

f <- function(x) {
  y1 = sin(30*((2*x-1)/2-0.4)^5)*cos(20*((2*x-1)/2-0.4))
  y2 = 1/3*sin(2*(2*x - 1))+2/3*exp(-30*(2*(2*x-1))^2)+1/3
  y3 = (sin(7.5*x)+1)/2
  return(cbind(y1, y2, y3))
}

Note that the function is defined in such a way that both its input, x, and output are matrices. The following figure shows the true functional forms of the three outputs of the simulator over [0,1][0, 1]:

dense_x <- seq(0, 1, length = 200)
dense_y <- f(dense_x)
output1 <- data.frame('x' = dense_x, 'y' = dense_y[,1])
output2 <- data.frame('x' = dense_x, 'y' = dense_y[,2])
output3 <- data.frame('x' = dense_x, 'y' = dense_y[,3])
p1 <- ggplot(data = output1, aes(x = x, y = y)) + geom_line(color = 'dodgerblue2') + ggtitle('Output 1') + theme(plot.title = element_text(size = 10))
p2 <- ggplot(data = output2, aes(x = x, y = y)) + geom_line(color = '#E31A1C') + ggtitle('Output 2') + theme(plot.title = element_text(size = 10))
p3 <- ggplot(data = output3, aes(x = x, y = y)) + geom_line(color = 'green4') + ggtitle('Output 3') + theme(plot.title = element_text(size = 10))
wrap_plots(list(p1, p2, p3)) + plot_annotation(title = 'Synthetic Simulator')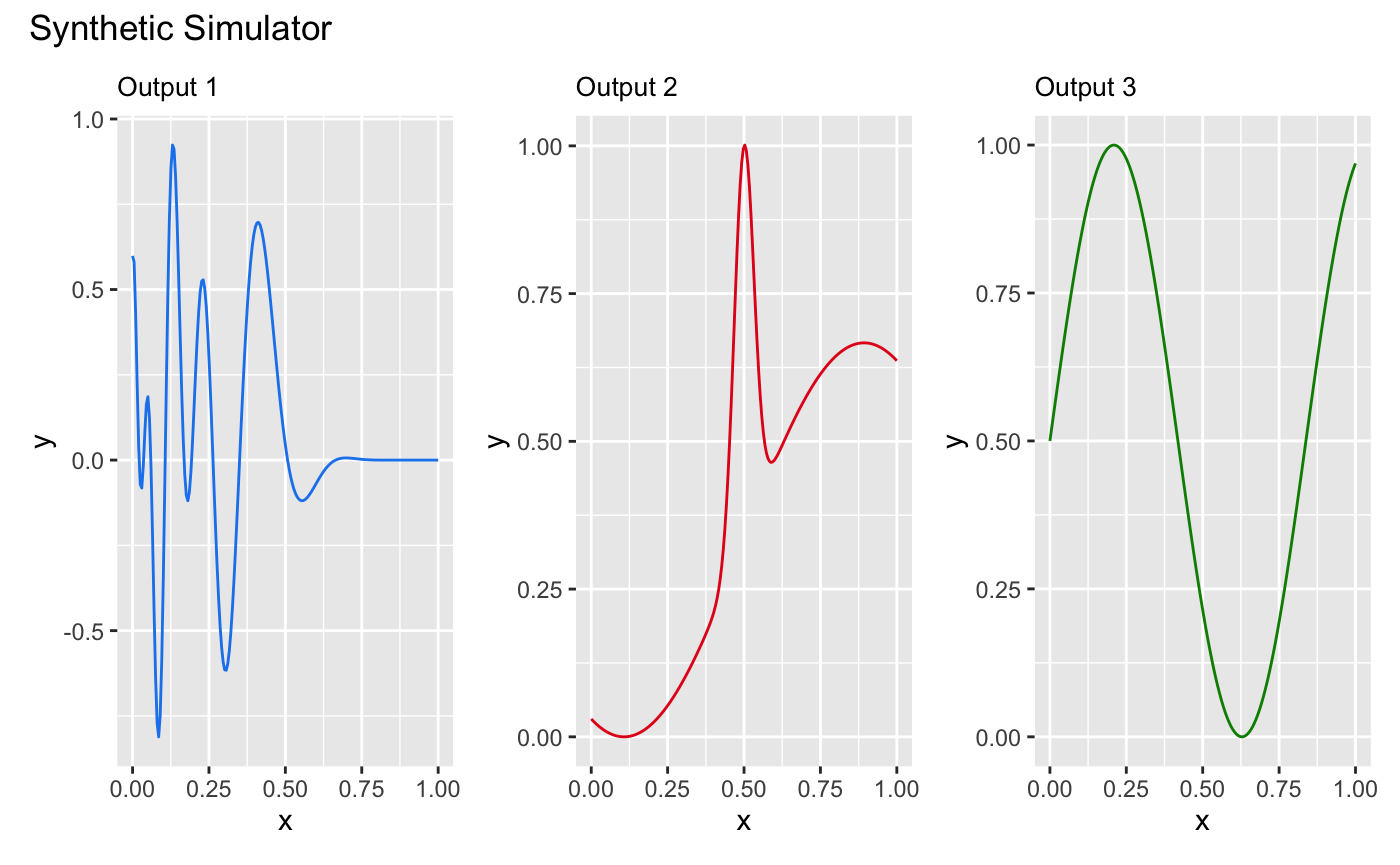

We now specify a seed with set_seed() from the package for reproducibility

set_seed(9999)

and generate an initial design with 5 design points using a maximin Latin hypercube sampler:

X <- maximinLHS(5, 1)
Y <- f(X)

We generate a validation dataset to track and stop the sequential design:

validate_x <- maximinLHS(200, 1)
validate_y <- f(validate_x)

Construct a bundle of DGP emulators

Before we start the sequential design, we build three DGP emulators that emulate the three outputs of the simulator f independently:

m1 <- dgp(X, Y[,1], connect = F)
## Auto-generating a 2-layered DGP structure ... done
## Initializing the DGP emulator ... done
## Training the DGP emulator: 
## Iteration 500: Layer 2: 100%|██████████| 500/500 [00:01<00:00, 335.63it/s]
## Imputing ... done
m2 <- dgp(X, Y[,2], connect = F)
## Auto-generating a 2-layered DGP structure ... done
## Initializing the DGP emulator ... done
## Training the DGP emulator: 
## Iteration 500: Layer 2: 100%|██████████| 500/500 [00:01<00:00, 294.20it/s]
## Imputing ... done
m3 <- dgp(X, Y[,3])
## Auto-generating a 2-layered DGP structure ... done
## Initializing the DGP emulator ... done
## Training the DGP emulator: 
## Iteration 500: Layer 2: 100%|██████████| 500/500 [00:01<00:00, 387.69it/s]
## Imputing ... done

Note that we have the global connection turned off for the first two DGP emulators because we found that this yields better emulation performance. We then build a bundle of the three DGP emulators using pack():

m <- pack(m1, m2, m3)

Sequential design for the emulator bundle

To begin sequential design, we first specify the limit of each input:

lim <- c(0, 1)

and set a target RMSE to stop the sequential design:

target <- 0.01

Here we choose 0.01 because it is equivalent to 1% normalized error given that the ranges of both outputs are [0,1]. We can set different targets for different outputs, e.g., by setting target <- c(0.005, 0.02, 0.01).

We start the first-wave of the sequential design with 10 steps:

# 1st wave of the sequential design with 10 steps
m <- design(m, N = 10, limits = lim, f = f, x_test = validate_x, y_test = validate_y, target = target)
## Initializing ... done
##  *  RMSE: 0.383722, RMSE: 0.154689, RMSE: 0.008984
## Iteration 1:
##  - Locating ... done
##  * Next design point (Emulator1): 0.207895
##  * Next design point (Emulator2): 0.235873
##  * Next design point (Emulator3): None (target reached)
##  - Updating and re-fitting ... done
##  - Validating ... done
##  *  RMSE: 0.337517, RMSE: 0.155087, RMSE: 0.008984
##  
##  ...
##  
## Iteration 10:
##  - Locating ... done
##  * Next design point (Emulator1): 0.430889
##  * Next design point (Emulator2): 0.479682
##  * Next design point (Emulator3): None (target reached)
##  - Updating and re-fitting ... done
##  - Validating ... done
##  *  RMSE: 0.120320, RMSE: 0.062365, RMSE: 0.008984
## Targets not reached for all emulators at the end of the sequential design.

It can be seen that at the first step, the DGP emulator for the third output has already reached the target, so no further refinements (i.e., additions of design points to the third DGP emulator) are performed for the remaining steps. By the end of the first wave, the DGP emulators for the first and second outputs have not yet reached the target. At this point, we can proceed to a second wave by repeating the command above. However, we demonstrate an alternative approach below, where we define an aggregation function (applicable to all built-in method functions of design()). This function aggregates criterion scores across the three outputs, ensuring that the same design points are added to all three emulators at each step, instead of selecting different design points for each emulator. Using the aggregation approach can be advantageous if the different outputs exhibit similar behavior with respect to the input, as it reduces number of simulations required at each iteration. However, if the outputs behave differently, it may be more effective to add distinct design points to each emulator to achieve lower errors more quickly.

We define the aggregation function g to compute a weighted average of the scores:

g <- function(x, weight){
  x[,1] <- x[,1]*weight[1]
  x[,2] <- x[,2]*weight[2]
  x[,3] <- x[,3]*weight[3]
  return(rowSums(x))
}

Since the third emulator has already reached the target, we assign zero weights to it and weights of 0.6 and 0.4 to the first and second emulators respectively:

weight <- c(0.6, 0.4, 0)

We now pass both the aggregate function, g(), and its weight argument to design() for a second wave of the sequential design with a further 15 steps:

# 2nd wave with 15 steps
m <- design(m, N = 15, limits = lim, f = f, x_test = validate_x, y_test = validate_y, aggregate = g, target = 0.01, weight = weight)
## Initializing ... done
##  *  RMSE: 0.120320, RMSE: 0.062365, RMSE: 0.008984
## Iteration 1:
##  - Locating ... done
##  * Next design point (Emulator1): 0.062821
##  * Next design point (Emulator2): 0.062821
##  * Next design point (Emulator3): None (target reached)
##  - Updating and re-fitting ... done
##  - Validating ... done
##  *  RMSE: 0.151946, RMSE: 0.061865, RMSE: 0.008984
##  
##  ...
##  
## Iteration 6:
##  - Locating ... done
##  * Next design point (Emulator1): 0.233155
##  * Next design point (Emulator2): None (target reached)
##  * Next design point (Emulator3): None (target reached)
##  - Updating and re-fitting ... done
##  - Validating ... done
##  *  RMSE: 0.014147, RMSE: 0.004410, RMSE: 0.008984
##  
##  ...
## 
## Iteration 8:
##  - Locating ... done
##  * Next design point (Emulator1): 0.009688
##  * Next design point (Emulator2): None (target reached)
##  * Next design point (Emulator3): None (target reached)
##  - Updating and re-fitting ... done
##  - Validating ... done
##  *  RMSE: 0.005913, RMSE: 0.004410, RMSE: 0.008984
Target reached! Sequential design stopped at step 8.

The first and the second emulators reached the target after iteration 8 and 5 of the second wave, respectively. The sequential design points of the three emulators can be plotted with draw():

draw(m, 'design')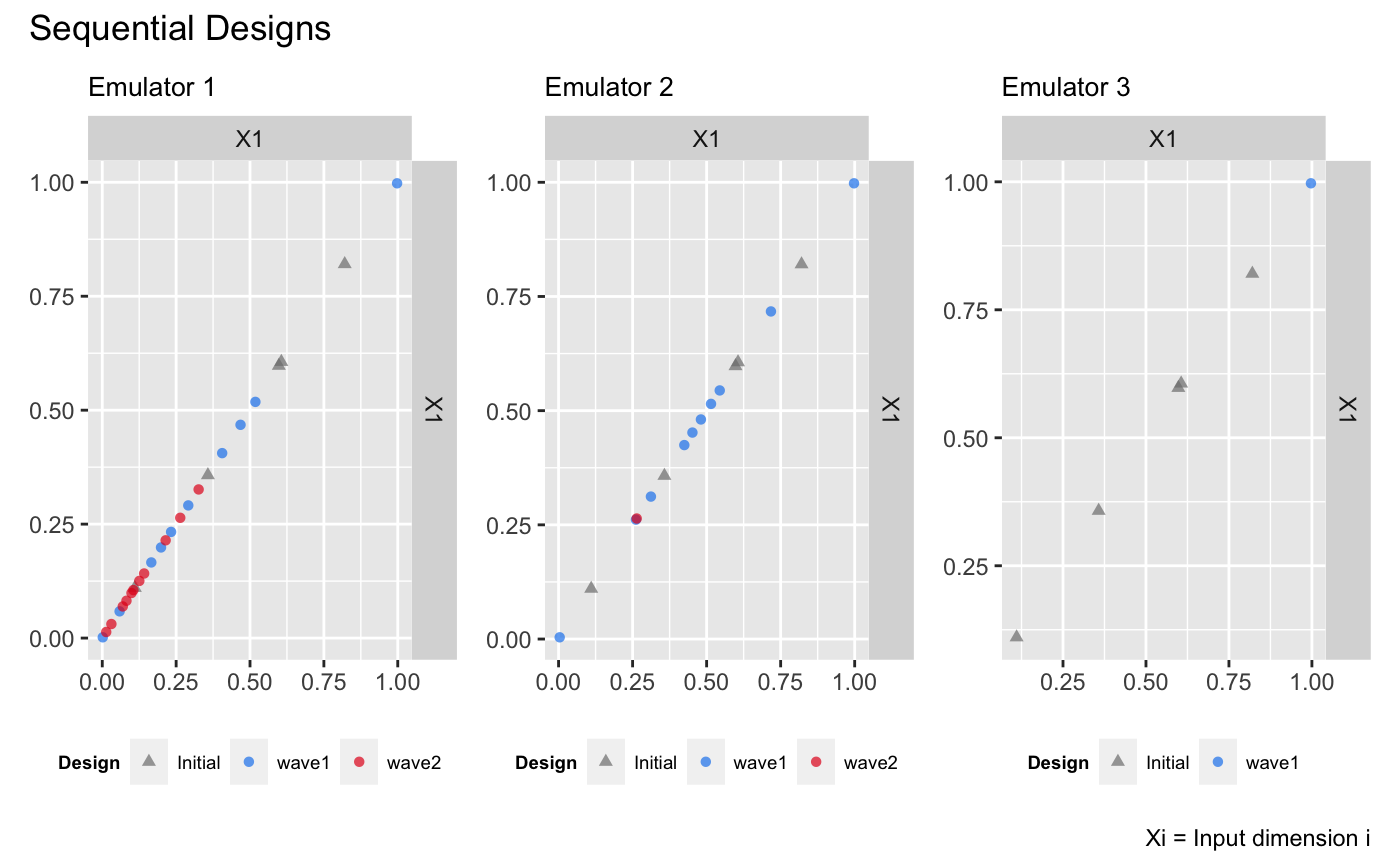

The figure above shows that, for the first emulator, most of the design points are added below 0.5, while for the second emulator, the design points are concentrated around 0.5. For the third emulator, the resulting design is space-filling. These design point distributions align with the functional complexities of the three outputs. However, in the second wave, which uses the aggregation function, additional points are added below 0.5 for the second emulator due to the higher weight assigned to the first emulator. These points may not be necessary for the second output, as its functional behavior does not require further refinement in that region. This observation aligns with the earlier argument that using the aggregation function to add the same design points to outputs with differing behaviors may not always be effective.

Comparison to DGP emulators with space-filling designs

We build three independent DGP emulators for the three outputs with static space-filling Latin hypercube designs (LHD) of size 10, 20, and 30 respectively:

# DGP emulators with a LHD of size 10
X1 <- maximinLHS(10, 1)
Y1 <- f(X1)
m11 <- dgp(X1, Y1[,1], connect = F, verb = F)
m12 <- dgp(X1, Y1[,2], connect = F, verb = F)
m13 <- dgp(X1, Y1[,3], verb = F)
# DGP emulator with a LHD of size 20
X2 <- maximinLHS(20, 1)
Y2 <- f(X2)
m21 <- dgp(X2, Y2[,1], connect = F, verb = F)
m22 <- dgp(X2, Y2[,2], connect = F, verb = F)
m23 <- dgp(X2, Y2[,3], verb = F)
# DGP emulator with a LHD of size 30
X3 <- maximinLHS(30, 1)
Y3 <- f(X3)
m31 <- dgp(X3, Y3[,1], connect = F, verb = F)
m32 <- dgp(X3, Y3[,2], connect = F, verb = F)
m33 <- dgp(X3, Y3[,3], verb = F)

We then extract their RMSEs

# validations of the first DGP emulator
m11 <- validate(m11, x_test = validate_x, y_test = validate_y[,1], verb = F)
m21 <- validate(m21, x_test = validate_x, y_test = validate_y[,1], verb = F)
m31 <- validate(m31, x_test = validate_x, y_test = validate_y[,1], verb = F)
rmse_static_1 <- data.frame('N' = c(10, 20, 30), 'rmse' = c(m11$oos$rmse, m21$oos$rmse, m31$oos$rmse), 'LHD' = c('lhd-10', 'lhd-20', 'lhd-30'))
# validations of the second DGP emulator
m12 <- validate(m12, x_test = validate_x, y_test = validate_y[,2], verb = F)
m22 <- validate(m22, x_test = validate_x, y_test = validate_y[,2], verb = F)
m32 <- validate(m32, x_test = validate_x, y_test = validate_y[,2], verb = F)
rmse_static_2 <- data.frame('N' = c(10, 20, 30), 'rmse' = c(m12$oos$rmse, m22$oos$rmse, m32$oos$rmse), 'LHD' = c('lhd-10', 'lhd-20', 'lhd-30'))
# # validations of the third DGP emulator
m13 <- validate(m13, x_test = validate_x, y_test = validate_y[,3], verb = F)
m23 <- validate(m23, x_test = validate_x, y_test = validate_y[,3], verb = F)
m33 <- validate(m33, x_test = validate_x, y_test = validate_y[,3], verb = F)
rmse_static_3 <- data.frame('N' = c(10, 20, 30), 'rmse' = c(m13$oos$rmse, m23$oos$rmse, m33$oos$rmse), 'LHD' = c('lhd-10', 'lhd-20', 'lhd-30'))

and add them to the sequential design validation plot (in log-scale) for comparison:

p <- draw(m, type = 'rmse', log = T) 
p[[1]] <- p[[1]] + 
  geom_point(data = rmse_static_1, mapping = aes(x = N, y = rmse, group = LHD, shape = LHD), color = '#E69F00', size = 1.5) +
  scale_shape_manual(values = c(3, 4, 8))
p[[2]] <- p[[2]] +
  geom_point(data = rmse_static_2, mapping = aes(x = N, y = rmse, group = LHD, shape = LHD), color = '#E69F00', size = 1.5) +
  scale_shape_manual(values = c(3, 4, 8))
p[[3]] <- p[[3]] +
  geom_point(data = rmse_static_3, mapping = aes(x = N, y = rmse, group = LHD, shape = LHD), color = '#E69F00', size = 1.5) +
  scale_shape_manual(values = c(3, 4, 8))
p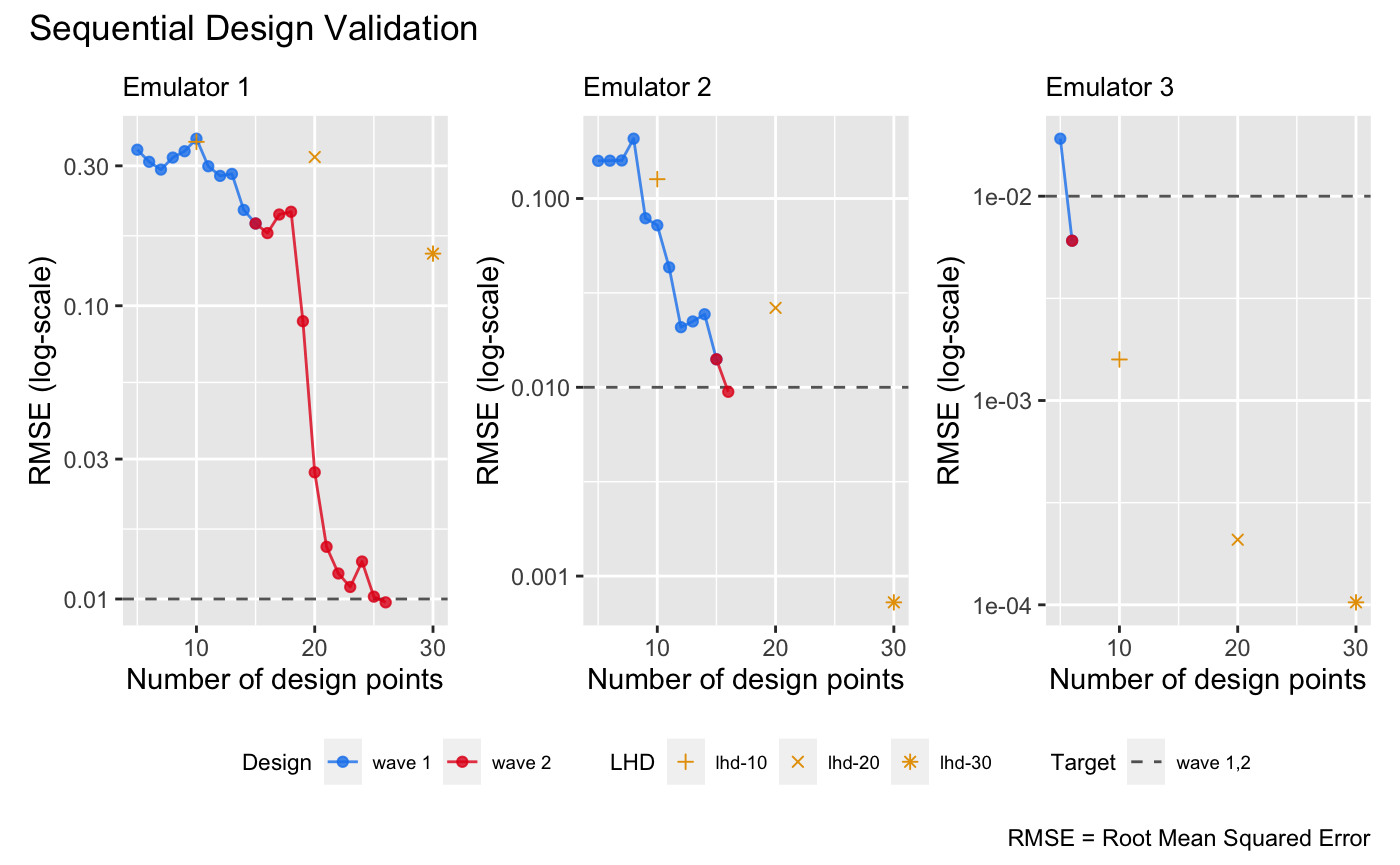

It can be seen from the plot above that sequential design is more efficient than batch space-filling design, achieving similar RMSE with fat fewer design points, particularly for the first emulator in the bundle.

See also

See Sequential Design I for the sequential design and automatic structure simplification of a DGP emulator on a 2D simulator.