DGP Classification

This vignette gives a demonstration of the package on classifying the popular iris data set (Anderson 1935).

Load packages and data

We start by loading required packages,

library(dgpsi)
library(dplyr)

We now load the iris data set,

data(iris)

and re-scale its four input variables to $[0,1]$.

iris <- iris %>%
  mutate(across(1:4, ~ (. - min(.)) / (max(.) - min(.))))

Before building a classifier, we set a seed with set_seed() from the package for reproducibility

set_seed(9999)

and split the data into training and testing:

test_idx <- sample(seq_len(nrow(iris)), size = 30)

train_data <- iris[-test_idx, ]
test_data <- iris[test_idx, ]

X_train <- as.matrix(train_data[, 1:4])
Y_train <- as.matrix(train_data[, 5])

X_test <- as.matrix(test_data[, 1:4])
Y_test <- as.matrix(test_data[, 5])

Construct and train a DGP classifier

We consider a three-layer DGP classifier, using a Matérn-2.5 kernel in the first layer and a squared exponential kernel in the second layer:

m_dgp <- dgp(X_train, Y_train, depth = 3, name = c('matern2.5', 'sexp'), likelihood = "Categorical")

## Auto-generating a 3-layered DGP structure ... done
## Initializing the DGP emulator ... done
## Training the DGP emulator: 
## Iteration 500: Layer 3: 100%|██████████| 500/500 [00:31<00:00, 15.63it/s]
## Imputing ... done

Visualizing the DGP object helps to clarify the layered structure for non-Gaussian (in this case categorical) likelihoods.

summary(m_dgp)

After the global inputs, the 3-layered DGP is comprised of 2 hidden layers containing GPs, and a “likelihood layer” that transforms each of the preceding GP nodes to one of the parameters required by the likelihood function. In this example, we have 3 possible categories and we use a softmax link function, so there are 3 parameters to set and the second layer has 3 GP nodes, one for each of them.

Validation

We are now ready to validate the classifier via validate() at 30 out-of-sample testing positions:

m_dgp <- validate(m_dgp, X_test, Y_test)

## Initializing the OOS ... done
## Calculating the OOS ... done
## Saving results to the slot 'oos' in the dgp object ... done

Finally, we visualize the OOS validation for the classifier:

plot(m_dgp, X_test, Y_test)

## Validating and computing ... done
## Post-processing OOS results ... done
## Plotting ... done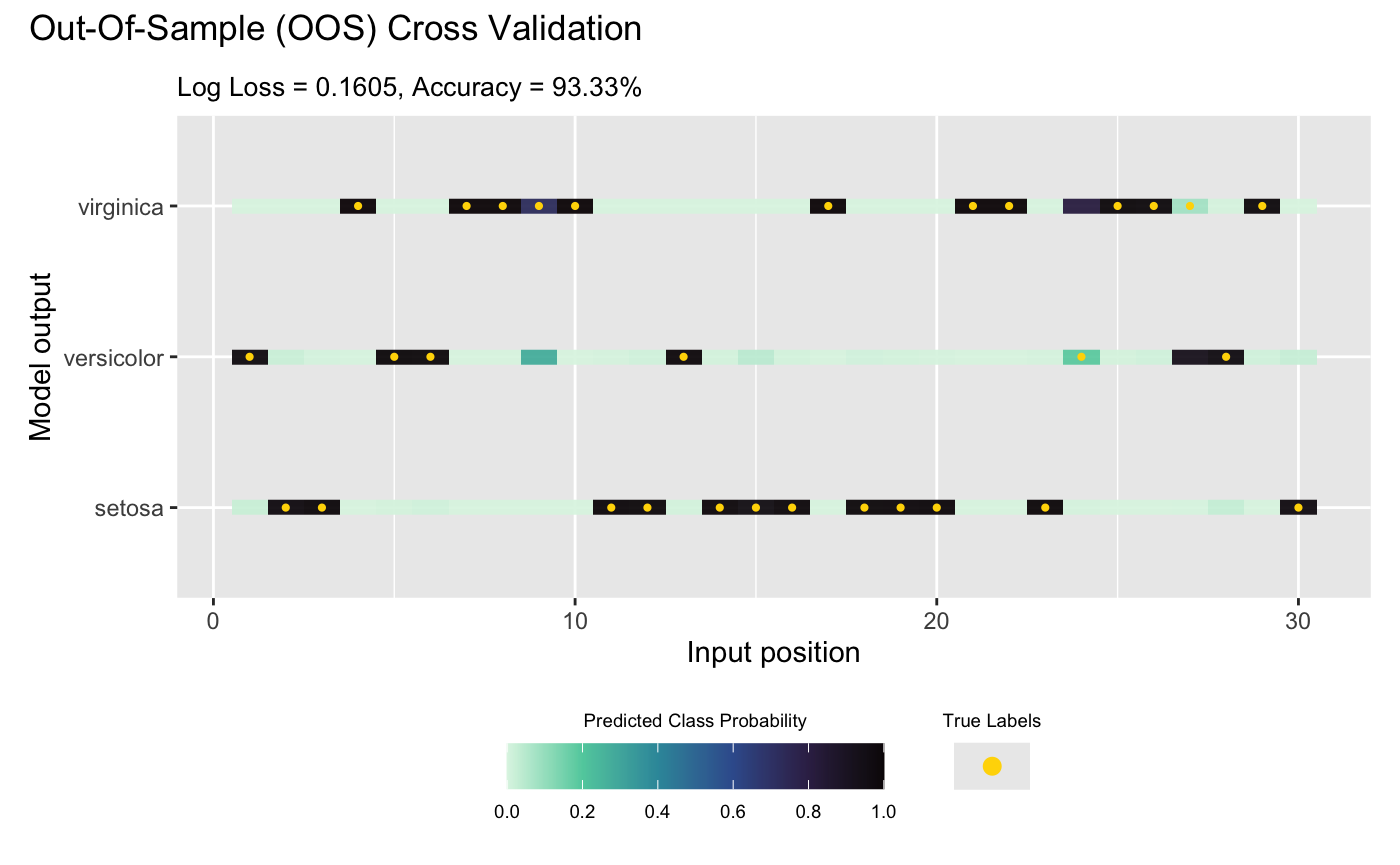

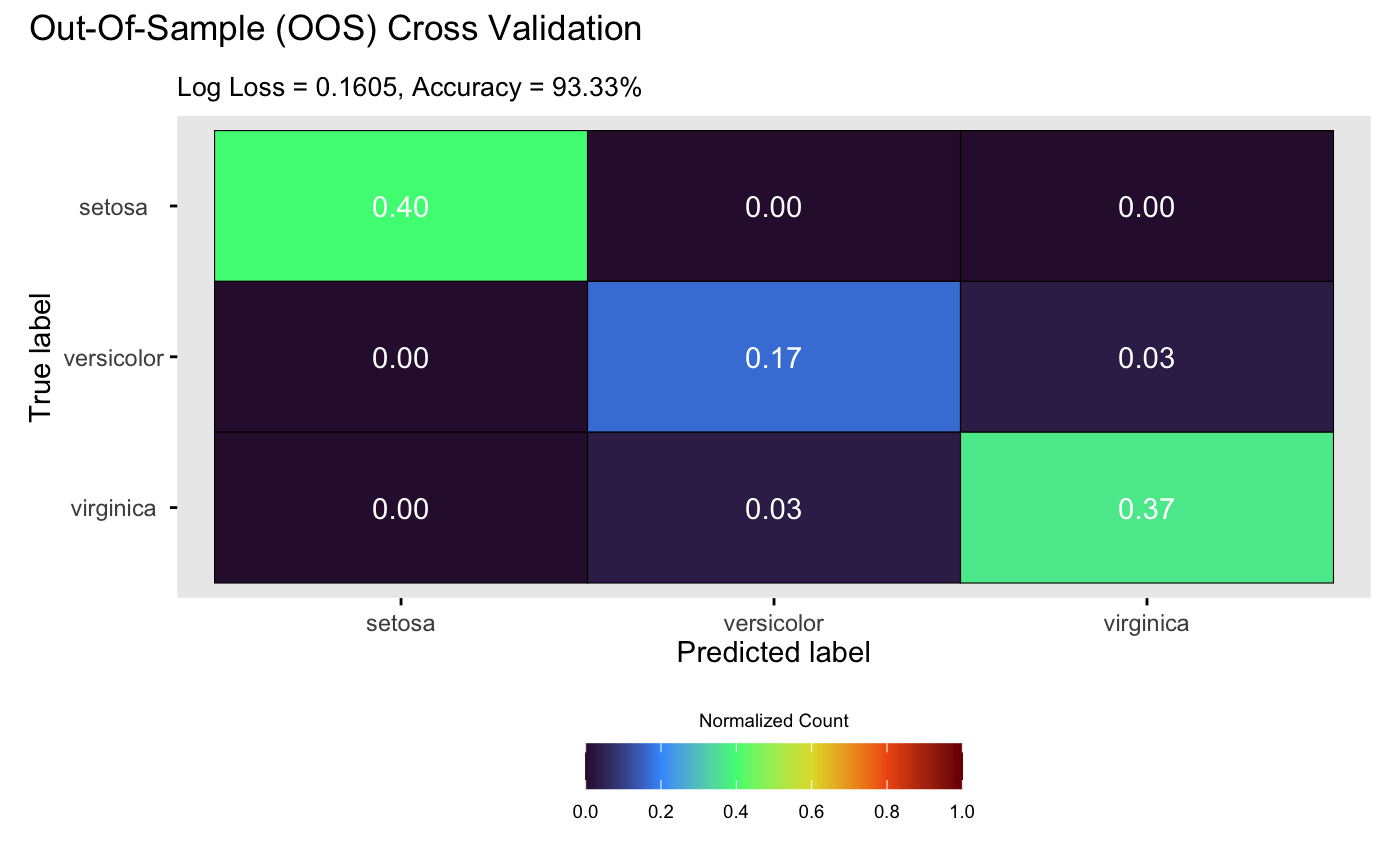
By default, plot() displays true labels against predicted label proportions at each input position. Alternatively, setting style = 2 in plot() generates a confusion matrix:

plot(m_dgp, X_test, Y_test, style = 2)

## Validating and computing ... done
## Post-processing OOS results ... done
## Plotting ... done

References

Anderson, Edgar. 1935. “The Irises of the Gaspe Peninsula.” Bulletin of American Iris Society 59: 2–5.