Skip to contents

Bayesian Optimization

Source: vignettes/bayes_opt.Rmd
bayes_opt.Rmd

This vignette demonstrates how to utilize and repurpose the design() function in dgpsi to implement Bayesian optimization using the (D)GP surrogate models provided by the package.

Load the packages

Define the target function

We consider a version of the Shubert function (Surjanovic and Bingham 2013) defined over the domain [0,1]2[0,1]^2 as follows:

shubert <- function(x)
{
  N <- nrow(x)
  x1 <- x[,1] * 4 - 2
  x2 <- x[,2] * 4 - 2
  ii <- c(1:5)
  
  y <- sapply(1:N, function(i) {
    sum(ii * cos((ii+1)*x1[i]+ii)) * sum(ii * cos((ii+1)*x2[i]+ii))
    })
  
  y <- matrix(y, ncol = 1)
  return(y)
}

To pass the Shubert function to design(), we defined it such that both its input x and output are matrices. Next, we generate the contour of the Shubert function:

x1 <- seq(0, 1, length.out = 200)
x2 <- seq(0, 1, length.out = 200)
dat <- expand_grid(x1 = x1, x2 = x2)
dat <- mutate(dat, f = shubert(cbind(x1, x2)))
ggplot(dat, aes(x1, x2, fill = f)) + geom_tile() + 
  scale_fill_continuous(type = "viridis")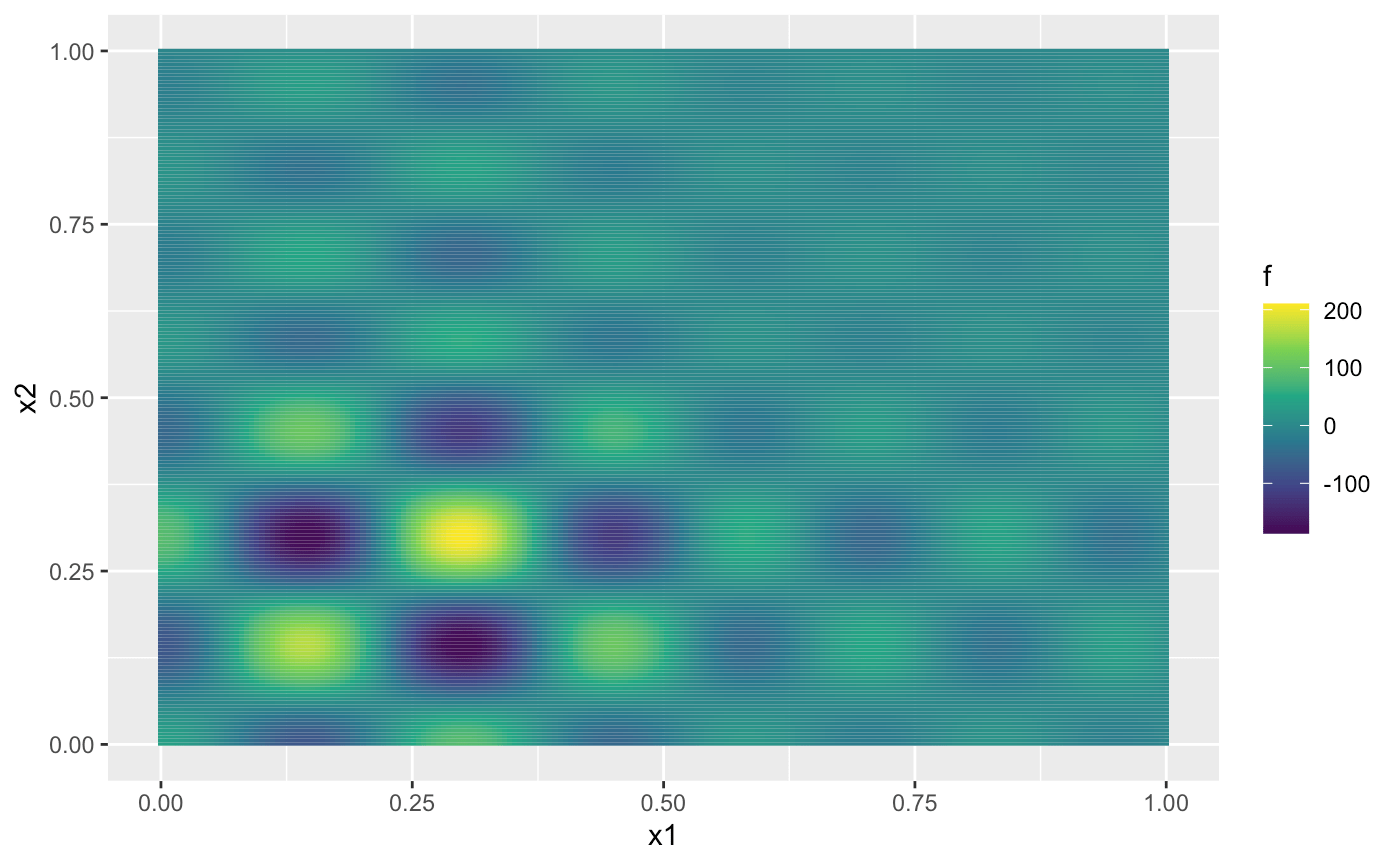

From the figure above, we can observe that the Shubert function has several local minima and two global minima located at (0.1437, 0.2999) and (0.2999, 0.1437), both with values around -186.7309. In the remainder of this vignette, we will use Expected Improvement (EI) as the acquisition function to identify the global minima.

Initial emulator construction

To ensure the reproducibility of this vignette, we set a seed using the set_seed() function from the package:

Next, we generate an initial design of 20 points using the maximin Latin hypercube sampler:

X <- maximinLHS(20, 2)
Y <- shubert(X)

to construct the initial DGP surrogate model of the Shubert function:

m <- dgp(X, Y, name = 'matern2.5')
## Auto-generating a 2-layered DGP structure ... done
## Initializing the DGP emulator ... done
## Training the DGP emulator: 
## Iteration 500: Layer 2: 100%|██████████| 500/500 [00:02<00:00, 249.19it/s]
## Imputing ... done

Bayesian optimization using Expected Improvement (EI)

To begin Bayesian optimization with design(), we first need to define the Expected Improvement (EI) acquisition function, adhering to the rules specified for the method argument in design():

ei <- function(object, limits, n_starts = 10, ...) {
  # Expected Improvement (EI) function
  ei_function <- function(x) {
    x <- matrix(x, nrow = 1)
    # Extract mean and variance from the 'object'
    pred <- predict(object, x, ...)$results
    mu <- pred$mean
    sigma <- sqrt(pred$var)
    
    # Handle numerical precision issues with very small sigma values
    sigma[sigma < 1e-10] <- 1e-10
    
    # Best observed minimum value
    best_value <- min(object$data$Y)
    
    # Calculate improvement
    improvement <- best_value - mu
    
    # Calculate Expected Improvement (EI)
    z <- improvement / sigma
    ei <- improvement * pnorm(z) + sigma * dnorm(z)
    ei <- ifelse(ei < 0, 0, ei)  # Ensure non-negative EI
    
    return(-ei)  # Return negative EI because `optim()` minimizes by default
  }
  
  # Number of input dimensions
  num_dims <- nrow(limits)
  
  # Generate initial points using Latin Hypercube Sampling (LHS)
  lhd_samples <- maximinLHS(n_starts, num_dims)
  lhd_points <- sapply(1:num_dims, function(i) {
    limits[i, 1] + lhd_samples[, i] * (limits[i, 2] - limits[i, 1])
  })
  
  # Perform optimization with multiple starts using `optim()`
  results <- lapply(1:n_starts, function(i) {
    optim(
      par = lhd_points[i, ],
      fn = ei_function,
      method = "L-BFGS-B",
      lower = limits[, 1],
      upper = limits[, 2]
    )
  })
  
  # Find the result with the minimum (most negative) EI
  best_result <- results[[which.min(sapply(results, `[[`, "value"))]]
  
  # Return the next best point `x` as a single-row matrix
  return(matrix(best_result$par, nrow = 1))
}

The ei function defined above takes the emulator as its first argument, object, along with the additional arguments: limits, a two-column matrix where the first column specifies the lower bounds and the second column specifies the upper bounds of the input dimensions, and n_starts, which defines the number of multi-start points used to search for the location corresponding to the minimum (most negative) EI. You can, of course, replace ei with your own acquisition function, provided it adheres to the rules of the method argument in design() (see ?design for details).

To track the identified minimum value of the Shubert function during Bayesian optimization, we define a monitor function, opt_monitor, to be passed to the eval argument of design():

opt_monitor <- function(object) {
  return(min(object$data$Y))
}

The domain of the input for the Shubert function, within which the global minima are searched by the Bayesian optimization, is defined as [0,1]2[0,1]^2:

lim <- rbind(c(0, 1), c(0, 1))

With all the ingredients ready, we can now run the Bayesian optimization using design() with 80 iterations:

m <- design(m, N = 80, limits = lim, f = shubert, method = ei, eval = opt_monitor)
## Initializing ... done
##  * Metric: -125.203479
## Iteration 1:
##  - Locating ... done
##  * Next design point: 0.352375 0.142570
##  - Updating and re-fitting ... done
##  - Validating ... done
##  * Metric: -125.203479
## 
## ...
## 
## Iteration 6:
##  - Locating ... done
##  * Next design point: 0.299331 0.125606
##  - Updating and re-fitting ... done
##  - Transiting to a GP emulator ... done
##  - Validating ... done
##  * Metric: -186.039545
## 
## ...
## 
## Iteration 80:
##  - Locating ... done
##  * Next design point: 0.907645 0.000000
##  - Updating and re-fitting ... done
##  - Validating ... done
##  * Metric: -186.728582

During the Bayesian optimization, our dynamic pruning mechanism transitioned the DGP emulator to a GP emulator at iteration 6, leading to faster optimizations in the remaining iterations while maintaining the emulator’s quality. After 80 iterations, we identified a minimum of the Shubert function with a value of -186.7286, which is very close to the global minimum of -186.7309. We can inspect the progress of the minima search conducted by design() by applying draw() to m:

draw(m) +
  plot_annotation(title = 'Bayesian Optimization Tracker') +
  labs(y = "Minimum Value") +
  # Add a horizontal line to represent the global minimum for benchmarking
  geom_hline(
    aes(yintercept = y, linetype = "Global Minimum"), # Global minimum
    data = data.frame(y = -186.7309),
    color = "#E31A1C",
    size = 0.5
  ) +
  scale_linetype_manual(
    values = c("Global Minimum" = "dashed"),
    name = "" # Remove the legend title
  )

The figure above shows that Bayesian optimization using our (D)GP emulator quickly identifies a low value of the Shubert function within 5 iterations. Notably, the lowest value, -186.7286, was achieved by design() after 48 iterations.

We can also inspect the locations identified during the process by applying draw() to m with type = 'design':

draw(m, type = 'design') + 
  plot_annotation(title = 'Bayesian Optimization Design') +
  # Highlight the global minima on the design plot
  geom_point(
    data = data.frame(
      .panel_x = c("X1", "X2"),  # x labels of panels
      .panel_y = c("X2", "X1"),  # y labels of panels
      X1 = c(0.1437, 0.2999),    # X1 values for the global minima
      X2 = c(0.2999, 0.1437)     # X2 values for the global minima
    ),
    aes(x = .panel_x, y = .panel_y),
    size = 1.25, 
    shape = 6,
    color = "#E31A1C"           
  )

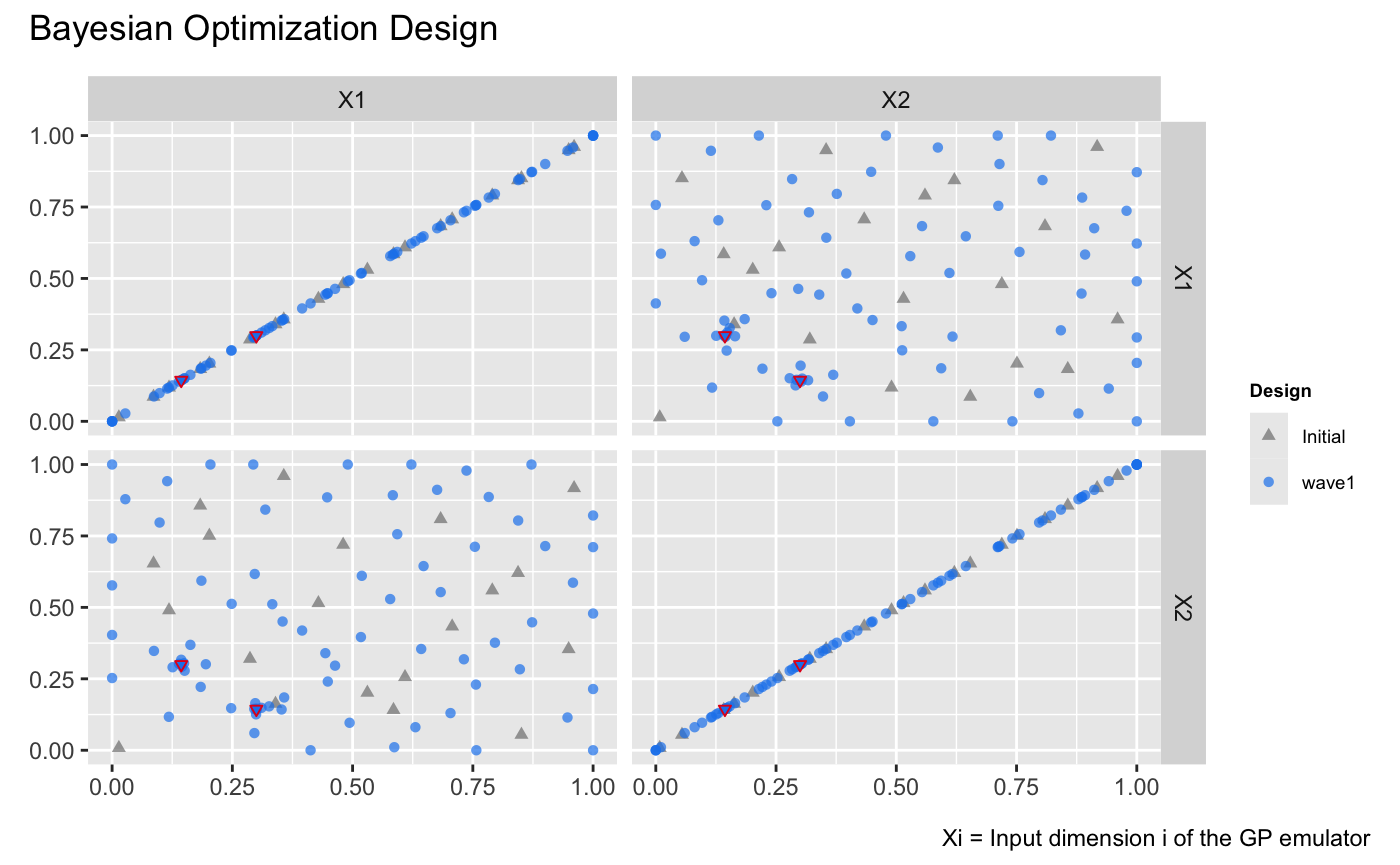
The figure above illustrates that Bayesian optimization successfully identifies the regions around the two global minima, represented as red inverted triangles, by adding design points concentrated near these two locations.

References

Surjanovic, Simon, and Derek Bingham. 2013. “Virtual Library of Simulation Experiments: Test Functions and Datasets.” https://www.sfu.ca/~ssurjano/index.html.