Skip to contents

Linked (D)GP Emulation

Source: vignettes/linked_DGP.Rmd
linked_DGP.Rmd

This vignette shows how to use the package to emulate a feed-forward system of three synthetic computer models.

Load the package

Construct a synthetic system

We consider the following synthetic system

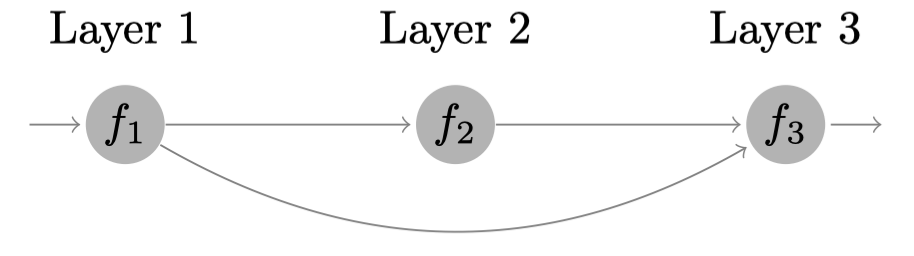
that involves three models defined by:

# Model 1
f1 <- function(x) {
  (sin(7.5*x)+1)/2
}
# Model 2
f2 <- function(x) {
  2/3*sin(2*(2*x - 1))+4/3*exp(-30*(2*(2*x-1))^2)-1/3  
}
# Model 3
f3 <- function(x) {
  x[1]*x[2]^2
}
# Linked Model 
f123 <- function(x) {
  f3(c(f1(x),f2(f1(x))))
}

We then specify a seed with set_seed() from the package for reproducibility

and generate 10 training data points for Model 1 and 15 training data points for Model 2 and 3:

# Training data for Model 1
X1 <- seq(0, 1, length = 10)
Y1 <- sapply(X1, f1)
# Training data for Model 2
X2 <- seq(0, 1, length = 15)
Y2 <- sapply(X2, f2)
# Training data for Model 3
X3 <- cbind(X2, Y2)
Y3 <- apply(X3, f3, MARGIN = 1)

Emulation of Model 1

We construct and train a GP emulator with Matérn-2.5 kernel:

m1 <- gp(X1, Y1, name = "matern2.5")
## Auto-generating a GP structure ... done
## Initializing the GP emulator ... done
## Training the GP emulator ... done

We now validate the trained GP emulator by plot() by LOO (alternatively, one can first use validate() to store the LOO results before plotting with plot()):

plot(m1)
## Initializing ... done
## Post-processing LOO results ... done
## Plotting ... done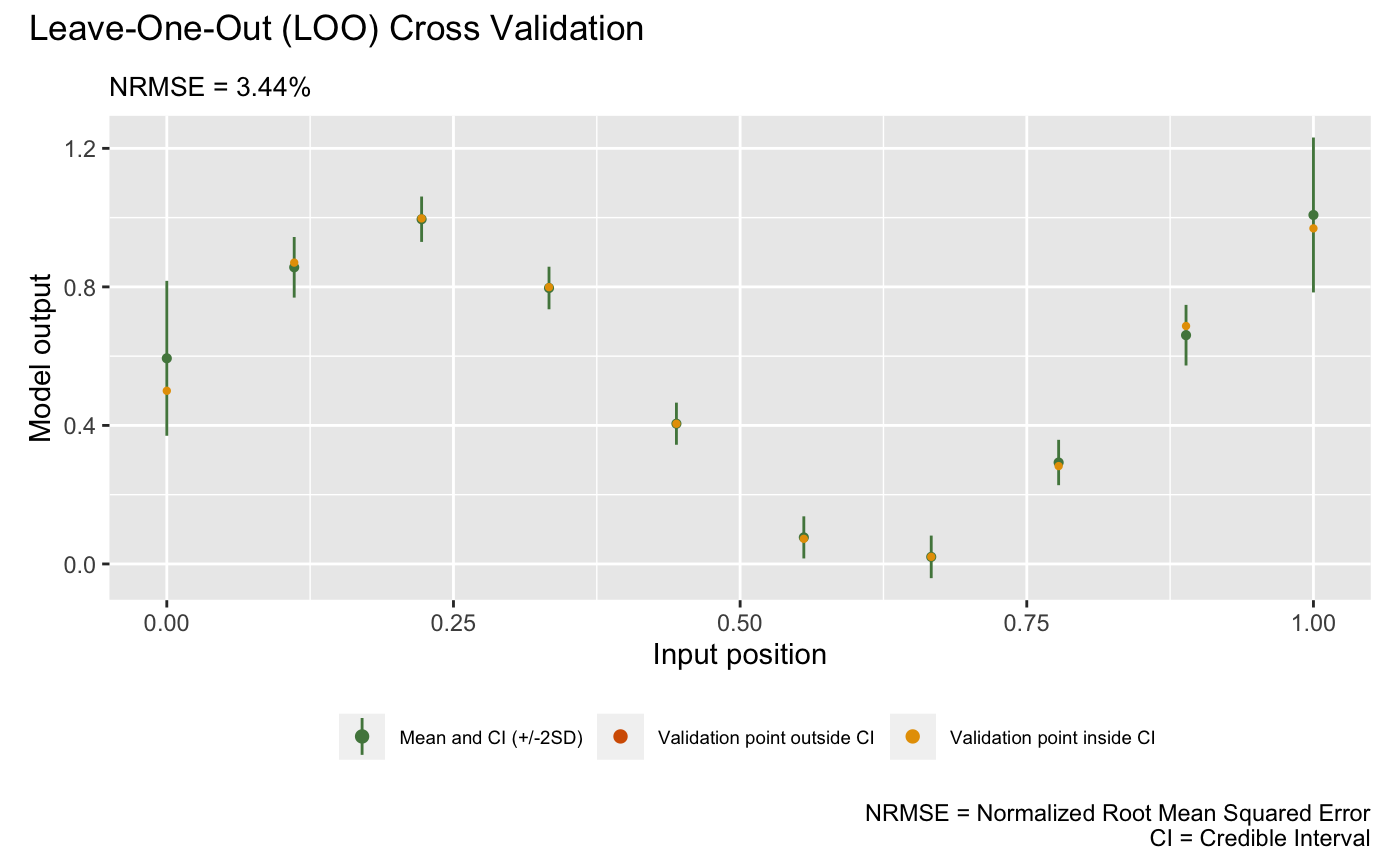

Since we will use m1 later for linked emulation, we must specify how it links to the emulators in the feeding layer through linked_idx in dgp(). Since m1 is in the first layer of the system, linked_idx refers to the column indices of the global input X that will feed into m1, and therefore we should have set linked_idx = c(1) in dgp() when we first constructed the emulator. Instead of re-training the emulator to provide this information, we can simply use set_linked_idx() to add this information to m1:

m1 <- set_linked_idx(m1, c(1))

Emulation of Model 2

We construct a two-layered DGP emulator with Matérn-2.5 kernels to emulate the Model 2:

m2 <- dgp(X2, Y2, depth = 2, name = "matern2.5", linked_idx = c(1))
## Auto-generating a 2-layered DGP structure ... done
## Initializing the DGP emulator ... done
## Training the DGP emulator:
## Iteration 500: Layer 2: 100%|██████████| 500/500 [00:01<00:00, 264.72it/s]
## Imputing ... done

Since all outputs of emulators in the first layer is from m1 and m2 uses the output from m1 as its input, we set linked_idx = c(1) in dgp() above.

The following plot visualizes the LOO of the trained DGP emulator m2:

plot(m2)
Initializing ... done
Post-processing LOO results ... done
Plotting ... done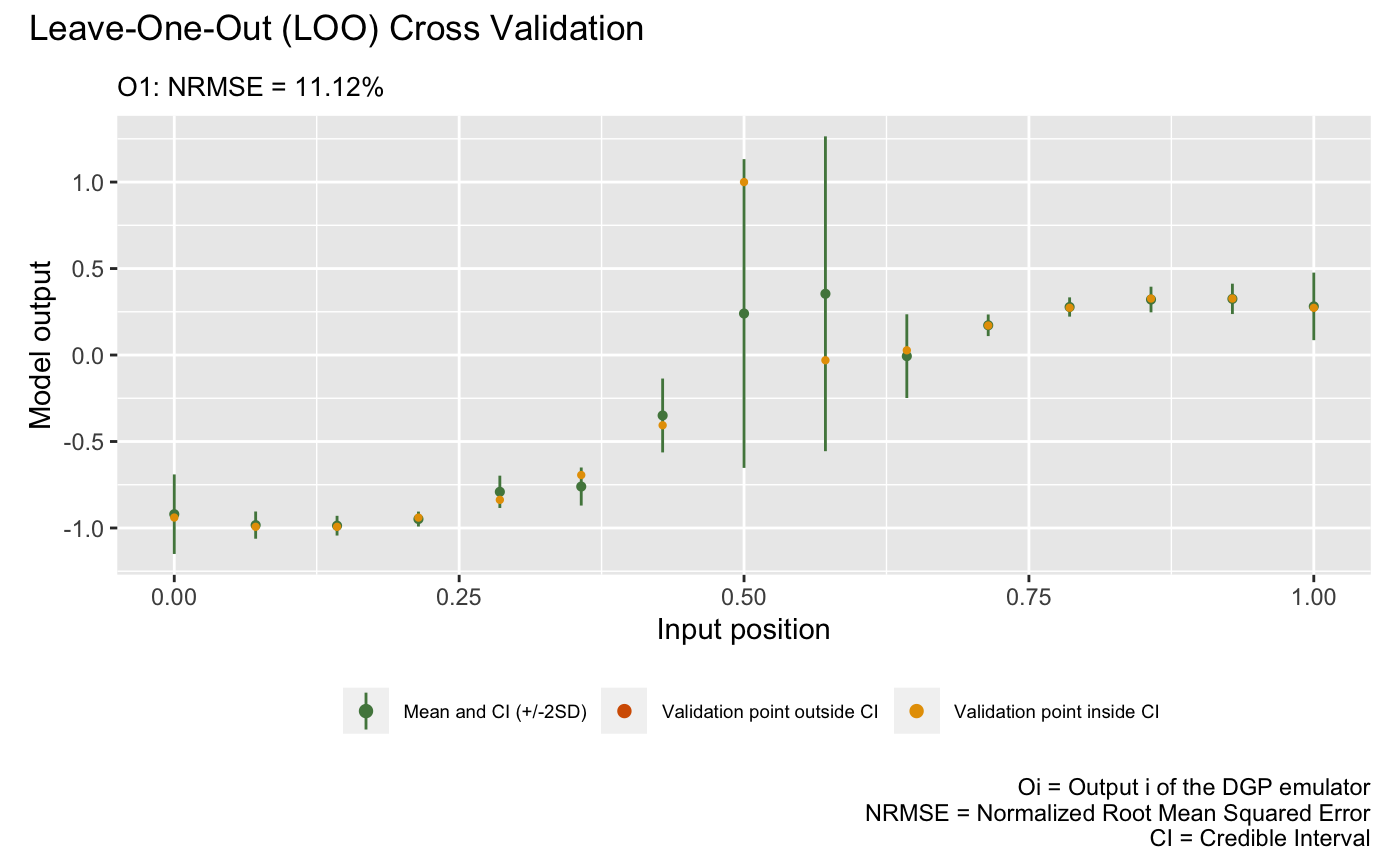

Emulation of Model 3

We now construct a three-layered DGP emulator with Matérn-2.5 kernels to emulate the Model 3:

m3 <- dgp( X3, Y3, depth = 3, name = "matern2.5", linked_idx = list( c(1), c(1) ) )
## Auto-generating a 3-layered DGP structure ... done
## Initializing the DGP emulator ... done
## Training the DGP emulator:
## Iteration 500: Layer 3: 100%|██████████| 500/500 [00:04<00:00, 104.80it/s]
## Imputing ... done

Since m3 takes both outputs from m1 in layer 1 and m2 in layer 2, we set linked_idx = list( c(1), c(1) ). The first vector in the list says that the output dimension 1 from all emulators (i.e., m1) in the first layer feeds into m3 and the second vector in the list says that the output dimension 1 from all emulators (i.e., m2) in the second layer feeds into m3. Note that the dimensions in X3 is ordered in consistent with linked_idx, i.e., the first and second columns of X3 correspond to the output of m1 and m2 respectively.

The following plot visualizes the LOO of the trained DGP emulator m3:

plot(m3)
Initializing ... done
Post-processing LOO results ... done
Plotting ... done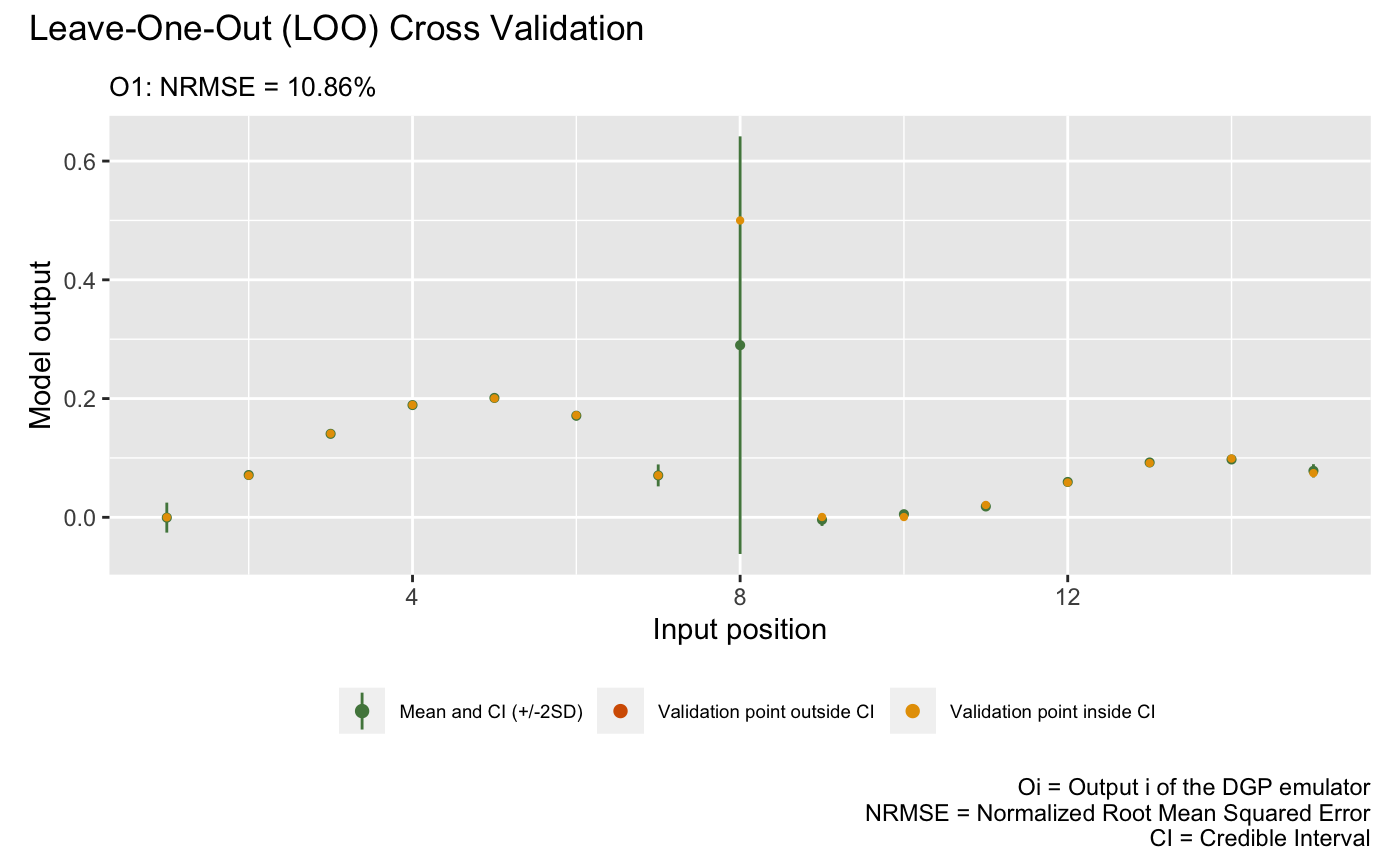

Emulation of Linked Model

With the GP emulator m1 (for Model 1), the DGP emulator m2 (for Model 2), and the DGP emulator m3 (for Model 3) at hand, we are now ready to build the linked emulator by first using combine() to construct the system hierarchy struc and then applying lgp() for the linked emulator.

struc <- combine(list(m1), list(m2), list(m3))
m_link <- lgp(struc)

Note that each layer of an emulator system is represented by a list. In our case, each layer contains a single emulator. Therefore, we need to put the corresponding emulator in a list using list().

We can check the relations between emulators in different layers by applying summary() to m_link:

summary(m_link)
## +-----------+--------------+------+----------------------------+-----------------+
## | Layer No. | Emulator No. | Type |         Connection         | External Inputs |
## +-----------+--------------+------+----------------------------+-----------------+
## |  Layer 1  |    Emu 1     |  GP  |     Global input: [1]      |       No        |
## |  Layer 2  |    Emu 1     | DGP  | Emu 1 in Layer 1: output 1 |       No        |
## |  Layer 3  |    Emu 1     | DGP  | Emu 1 in Layer 1: output 1 |       No        |
## |           |              |      | Emu 1 in Layer 2: output 1 |                 |
## +-----------+--------------+------+----------------------------+-----------------+
## 1. 'Connection' gives the indices of emulators and the associated output dimensions that are linked to the emulator referred by 'Layer No.' and 'Emulator No.'.
## 2. 'External Inputs' indicates if the emulator (referred by 'Layer No.' and 'Emulator No.') has external inputs that are not provided by the feeding emulators.

For comparison, we construct a GP emulator for the whole system by generating 15 training data points from Model 1 and Model 2:

X_gp <- seq(0, 1, length = 15)
Y_gp <- sapply(X_gp, f123)
m_gp <- gp(X_gp, Y_gp, name = 'matern2.5')
## Auto-generating a GP structure ... done
## Initializing the GP emulator ... done
## Training the GP emulator ... done

Finally, we validate both the GP emulator and the linked emulator at 300 testing data points over \([0,1]\):

# Testing input
test_x <- seq(0, 1, length = 300)
# Testing output
test_y <- sapply(test_x, f123)
# Validate GP emulator
m_gp <- validate(m_gp, x_test = test_x, y_test = test_y, verb = F)
# Validate linked emulator
m_link <- validate(m_link, x_test = test_x, y_test = test_y, verb = F)

and plot them to compare their emulation performances:

# GP emulator
plot(m_gp, x_test = test_x, y_test = test_y, type = 'line', verb = F) +
  plot_annotation(title = 'GP Emulator', theme = theme(plot.title = element_text(hjust = 0.5)))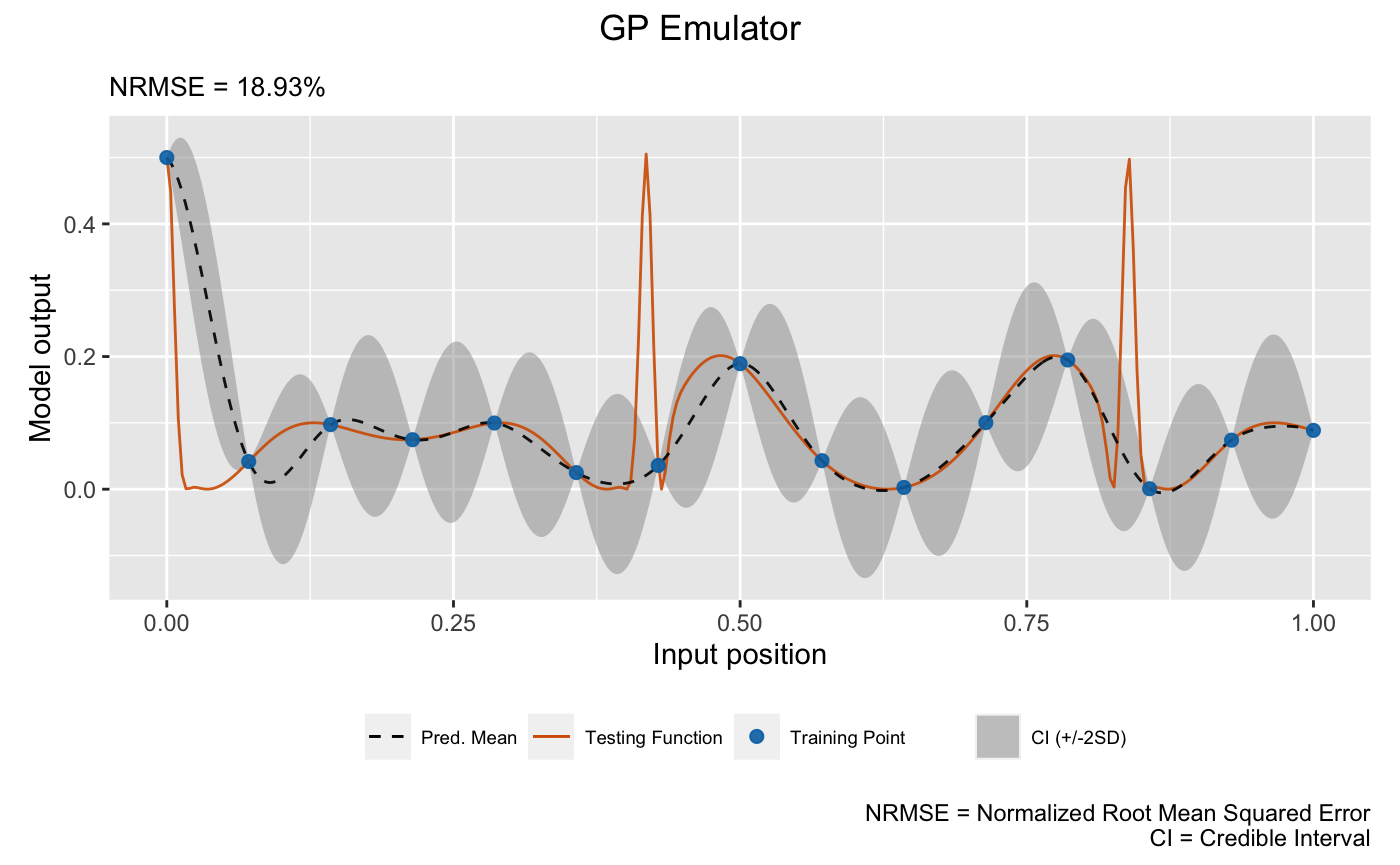

# Linked emulator
plot(m_link, x_test = test_x, y_test = test_y, type = 'line', verb = F) +
  plot_annotation(title = 'Linked Emulator', theme = theme(plot.title = element_text(hjust = 0.5)))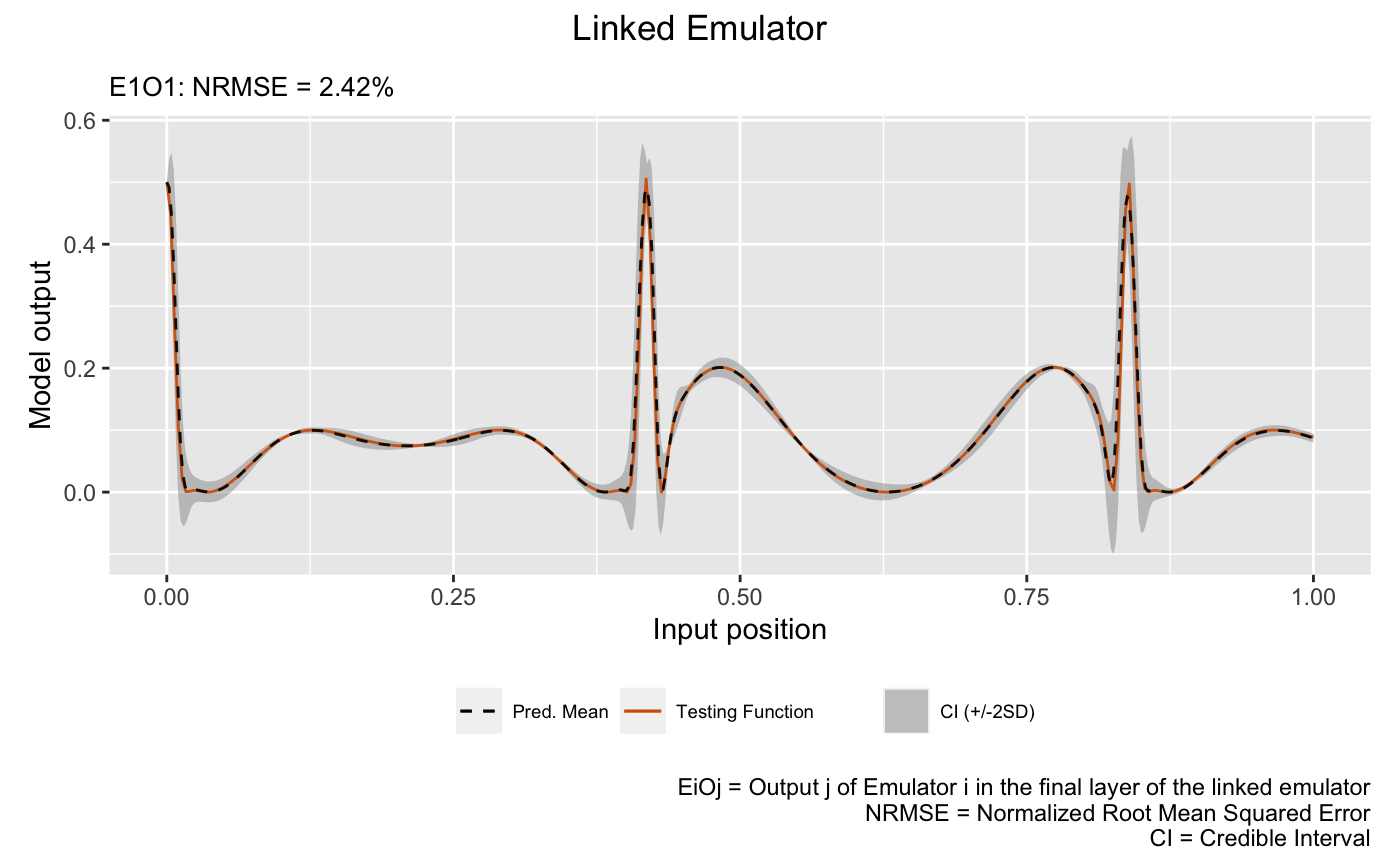

It can be seen from the above plots that the linked emulator outperforms the GP emulator with significantly better mean predictions and predictive uncertainties.

In real-life applications, we are rarely able to generate this many testing data points from the underlying computer simulators to evaluate the emulators over the whole input space. However, we are still able to retain some available realizations from the computer simulators for the linked emulator validation. Say we were able to afford 20 runs of the above linked computer system:

# OOS testing input
test_x_oos <- sample(seq(0, 1, length = 300), 20)
# OOS testing output
test_y_oos <- sapply(test_x_oos, f123)

Then, we can conduct OOS validations for the GP emulator:

plot(m_gp, test_x_oos, test_y_oos, style = 2)
## Initializing ... done
## Post-processing OOS results ... done
## Plotting ... done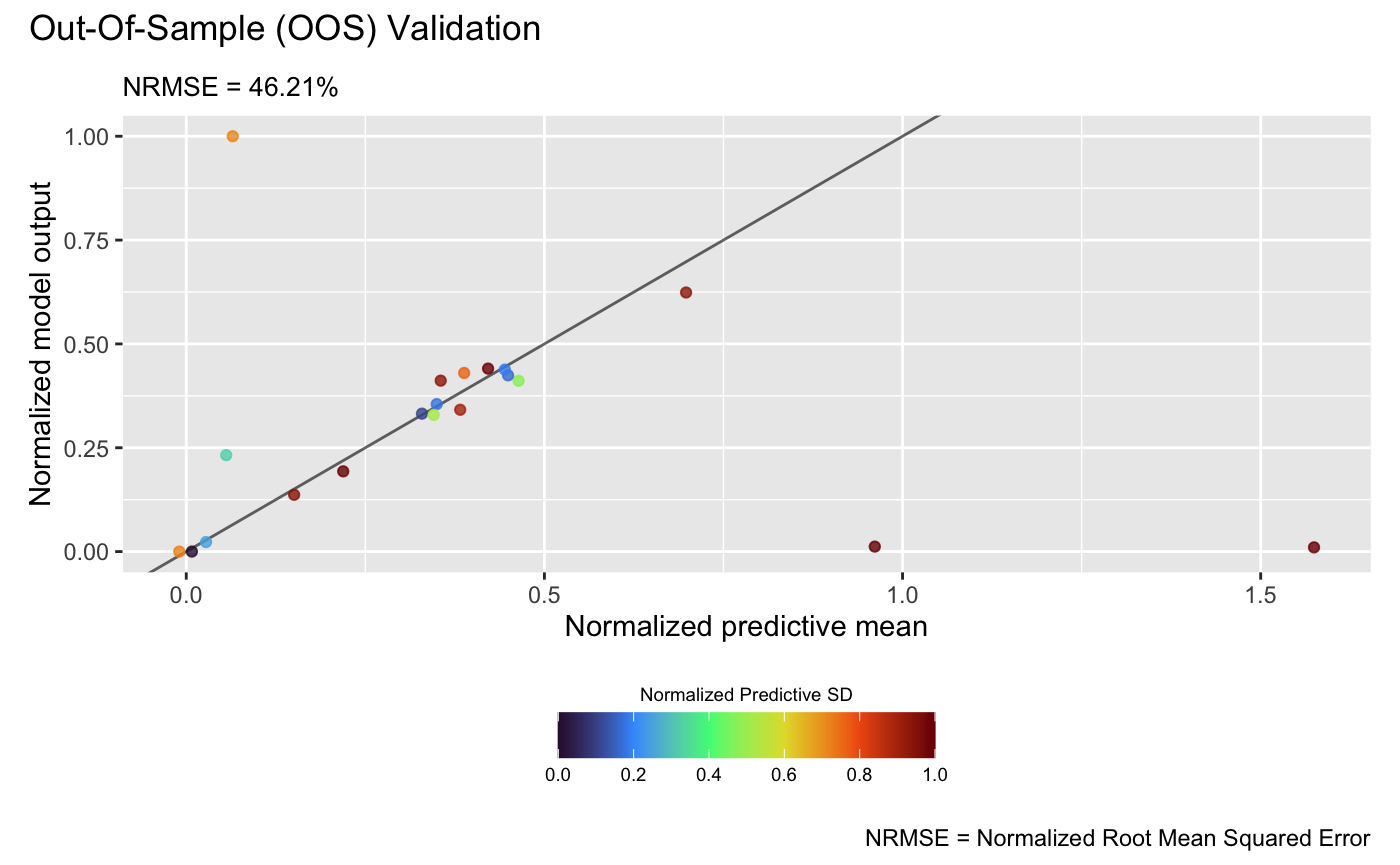

and the linked emulator:

plot(m_link, test_x_oos, test_y_oos, style = 2)
## Initializing ... done
## Post-processing OOS results ... done
## Plotting ... done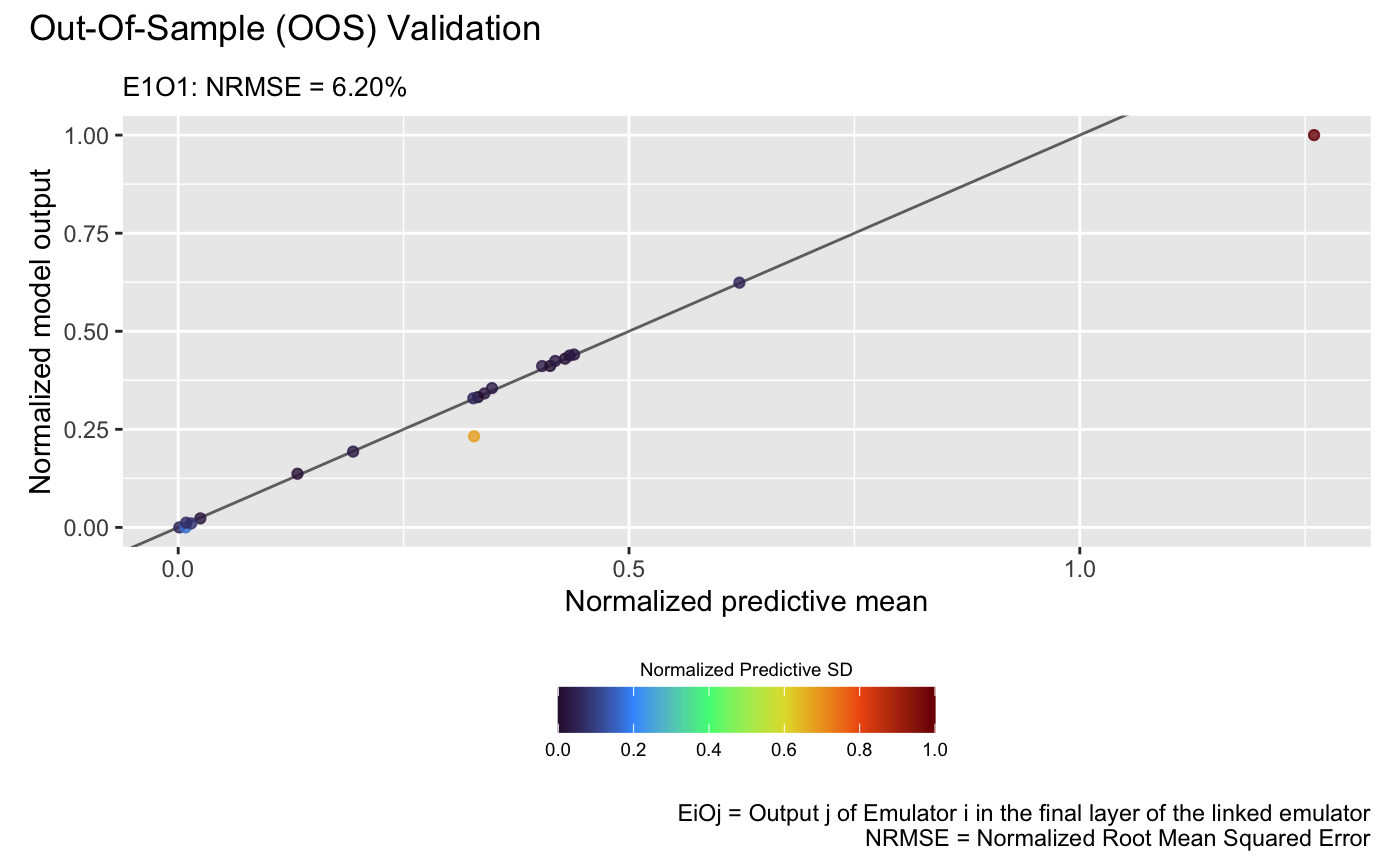

which show that the linked emulator outperforms the GP emulator with significantly better predictive accuracy and lower NRMSE.