Non-Gaussian Emulation • dgpsi

This vignette gives a demonstration of the package on emulating the popular motorcycle dataset (Silverman 1985).

Load packages and data

We start by loading packages:

library(dgpsi)
library(MASS)
library(ggplot2)
library(patchwork)

We now load the training data points,

X <- mcycle$times
Y <- mcycle$accel

scale them,

X <- (X - min(X))/(max(X)-min(X))
Y <- scale(Y, center = TRUE, scale = TRUE)

and plot them:

ggplot(data = data.frame(X = X, Y = Y), aes(x = X, y = Y)) +
  geom_point(shape = 16, size = 3) +
  labs(x = "Time", y = "Acceleration") +
  theme(axis.title = element_text(size = 13), 
        axis.text = element_text(size = 13))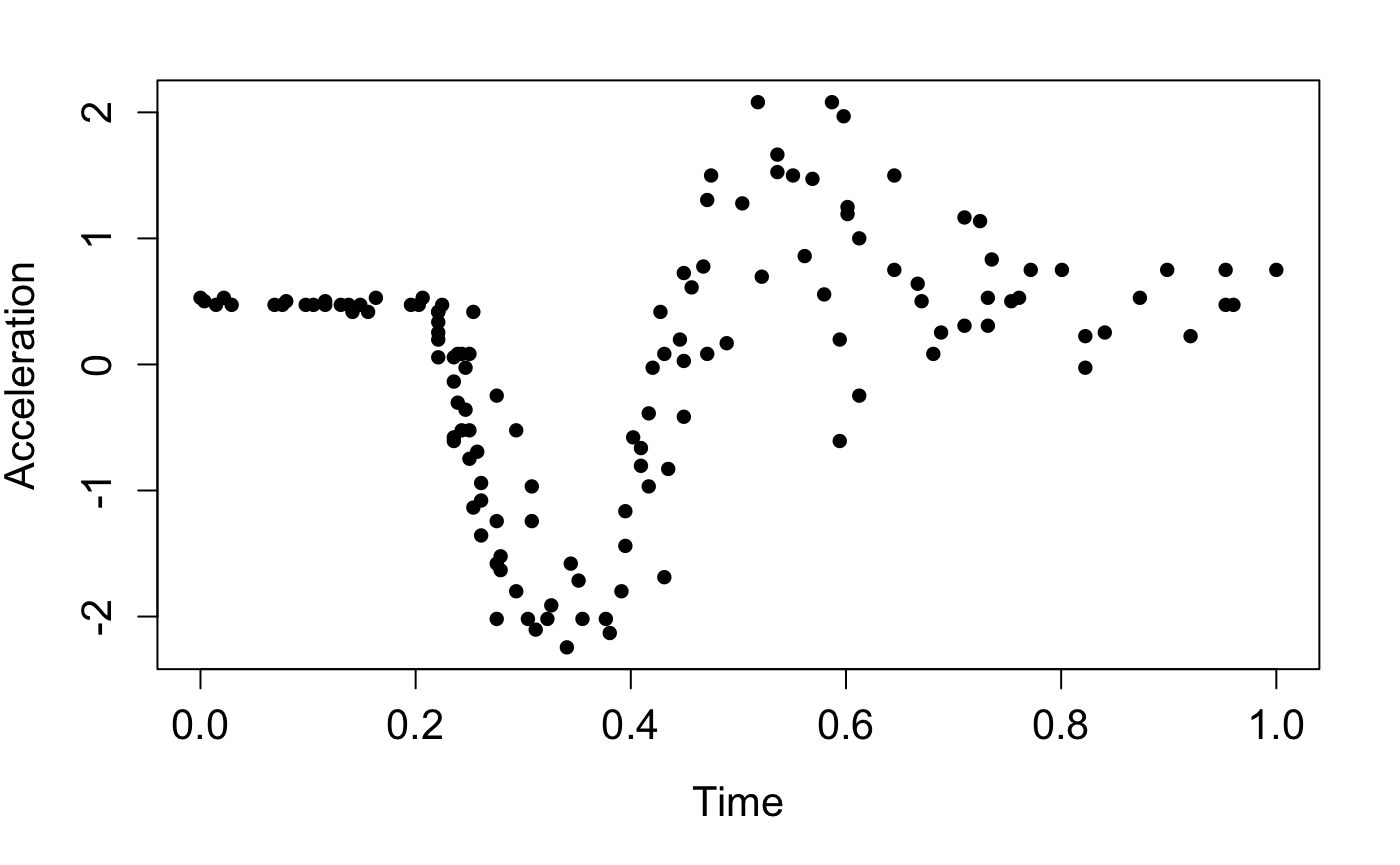

Before constructing an emulator, we first specify a seed with set_seed() from the package for reproducibility

set_seed(9999)

and split a training data set and a testing data set:

test_idx <- sample(seq_len(length(X)), size = 20)
train_X <- X[-test_idx]
train_Y <- Y[-test_idx,]
test_x <- X[test_idx]
test_y <- Y[test_idx,]

Construct and train a DGP emulator

We consider a three-layered DGP emulator with squared exponential kernels and heteroskedastic likelihood:

m_dgp <- dgp(train_X, train_Y, depth = 3, likelihood = "Hetero")

## Auto-generating a 3-layered DGP structure ... done
## Initializing the DGP emulator ... done
## Training the DGP emulator: 
## Iteration 500: Layer 3: 100%|██████████| 500/500 [00:14<00:00, 35.52it/s]
## Imputing ... done

We choose a heteroskedastic Gaussian likelihood by setting likelihood = "Hetero" since the data drawn in the plot show varying noise. We can use summary() to visualize the structure and specifications for the trained DGP emulator:

summary(m_dgp)

For comparison, we also build a GP emulator (by gp()) that incorporates homogeneous noise by setting nugget_est = T and the initial nugget value to $0.01$ :

m_gp <- gp(train_X, train_Y, nugget_est = T, nugget = 1e-2)

## Auto-generating a GP structure ... done
## Initializing the GP emulator ... done
## Training the GP emulator ... done

We can also summarize the trained GP emulator by summary():

summary(m_gp)

Validation

We are now ready to validate both emulators via validate() at the 20 out-of-sample testing positions generated earlier:

m_dgp <- validate(m_dgp, test_x, test_y)

## Initializing the OOS ... done
## Calculating the OOS ... done
## Saving results to the slot 'oos' in the dgp object ... done

m_gp <- validate(m_gp, test_x, test_y)

## Initializing the OOS ... done
## Calculating the OOS ... done
## Saving results to the slot 'oos' in the gp object ... done

Note that using validate() before plotting can save subsequent computations compared to simply invoking plot(), as validate() stores validation results in the emulator objects and plot() will use these, if it can, to avoid calculating them on the fly. Finally, we plot the OOS validation for the GP emulator:

plot(m_gp, test_x, test_y)

## Validating and computing ... done
## Post-processing OOS results ... done
## Plotting ... done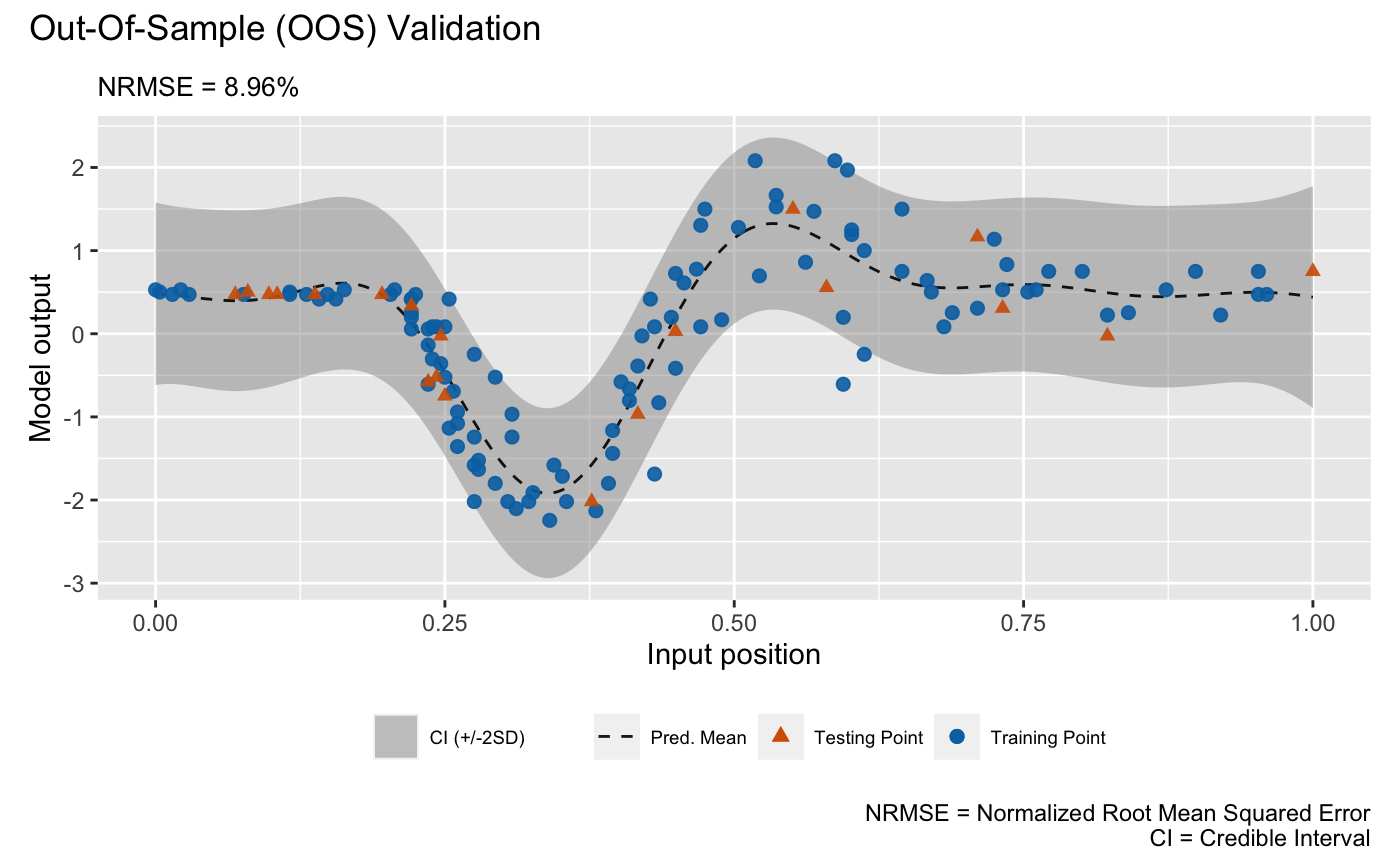

and for the DGP emulator:

plot(m_dgp, test_x, test_y)

## Validating and computing ... done
## Post-processing OOS results ... done
## Plotting ... done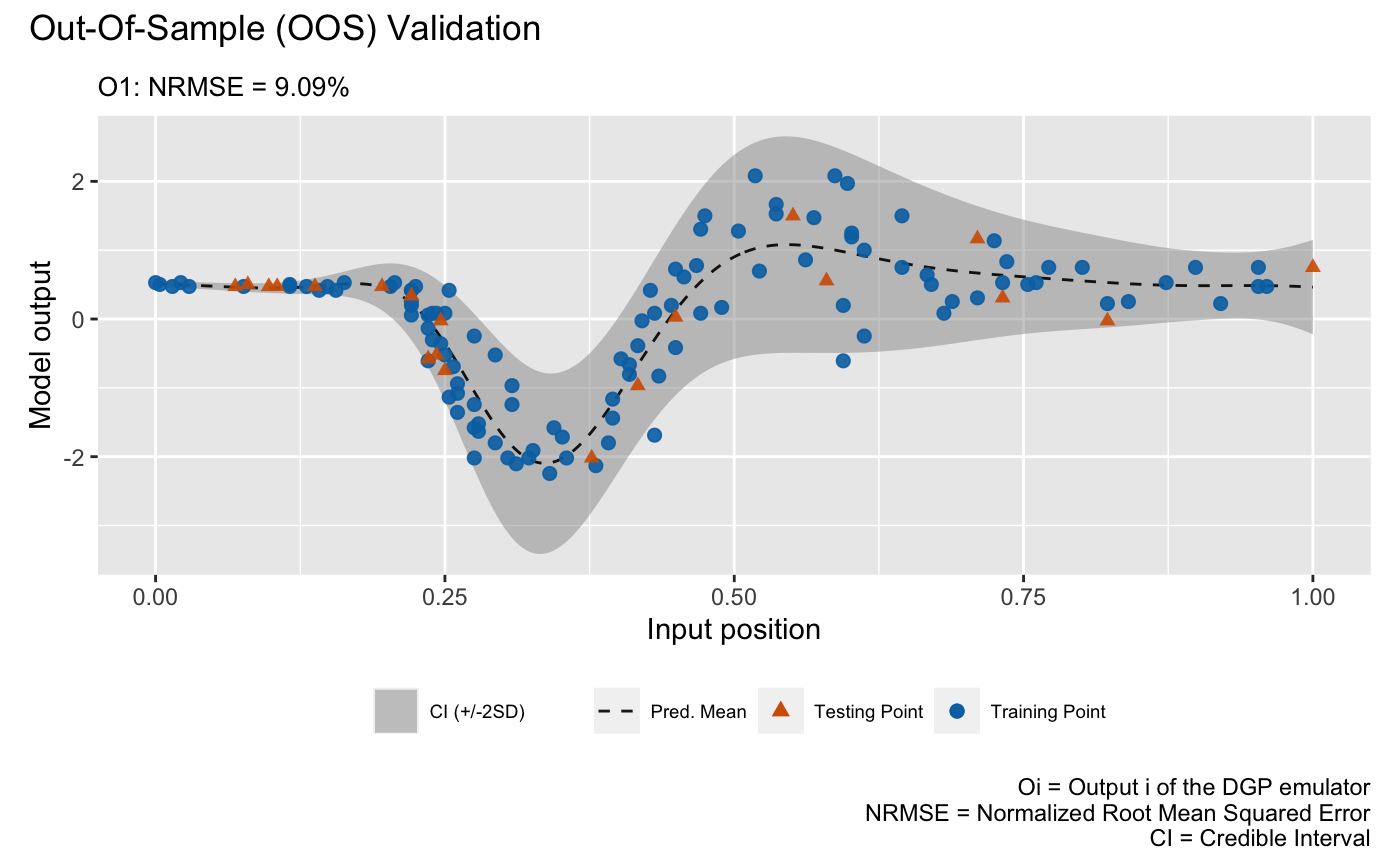

Note that we still need to provide test_x and test_y to plot() even they have already been provided to validate(). Otherwise, plot() will draw a LOO cross validation plot. The visualizations above show that the DGP emulator gives a better performance than the GP emulator on modeling the heteroskedastic noise embedded in the underlying data set, even though they have quite similar NRMSEs.

References

Silverman, Bernhard W. 1985. “Some Aspects of the Spline Smoothing Approach to Non-Parametric Regression Curve Fitting.” Journal of the Royal Statistical Society: Series B (Methodological) 47 (1): 1–21.