The dgpsi package offers a flexible toolbox for Gaussian
process (GP), deep Gaussian process (DGP), and linked (D)GP emulation.
In this guide, we show how to use the package to emulate a step function
using a three-layered DGP structure. Additional examples showcasing the
package’s functionality are available in the Articles
section of the package website. Topics include linked
DGPs, scalable
DGPs, DGPs
for classification, non-Gaussian
problems, sequential
design and active learning for (D)GPs, and Bayesian
optimization with (D)GPs. A detailed reference for all available
functions is provided in the Reference
section of the package website.
Set up the step function
dgpsi provides a function init_py() that
helps us set up, initialize, re-install, or uninstall the underlying
Python environment. We could run init_py() every time after
dgpsi is loaded to manually initiate the Python
environment. Alternatively, we could activate the Python environment by
simply executing a function from dgpsi. For example, the
Python environment will be automatically loaded after we run
set_seed() from the package to specify a seed for
reproducibility:
set_seed(9999)Define the step function:
and generate ten training data points:
Training
We now build and train a DGP emulator with three layers:
m <- dgp(X, Y, depth = 3)## Auto-generating a 3-layered DGP structure ... done
## Initializing the DGP emulator ... done
## Training the DGP emulator:
## Iteration 500: Layer 3: 100%|██████████| 500/500 [00:03<00:00, 148.10it/s]
## Imputing ... doneThe progress bar displayed shows how long it takes to finish
training. We are able to switch off the progress bar and the trace
information by setting verb = FALSE. Note that if we want
to train the DGP emulator m for additional iterations, we
can simply do m <- continue(m) instead of rebuilding the
DGP emulator.
The trained DGP emulator can be visualized using the
summary() function:
summary(m)The visualization gives key information about the trained DGP
emulator. Note that in the auto-generated emulator we have nugget terms
fixed to 1e-6 for all GP nodes because we are emulating a
deterministic step function (i.e., we would like our emulator to
interpolate training data points). The prior scales (i.e., variances)
for GP nodes in the first and second layers are fixed to
1.0 while that for the GP node in the final layer is
estimated due to its attachment to the output. For further information
on how to change the default settings to construct and train a DGP
emulator, see ?dgp.
At this point, you could use write() to save the
emulator m to a local file and then load it using
read() when you would like to make predictions from the
emulator, e.g., on another computer that also has the package
installed.
Validation
After we have the emulator, we can validate it by drawing the validation plots. There are two types of validation plots provided by the package. The first one is the Leave-One-Out (LOO) cross validation plot:
plot(m)## Validating and computing ... done
## Post-processing LOO results ... done
## Plotting ... done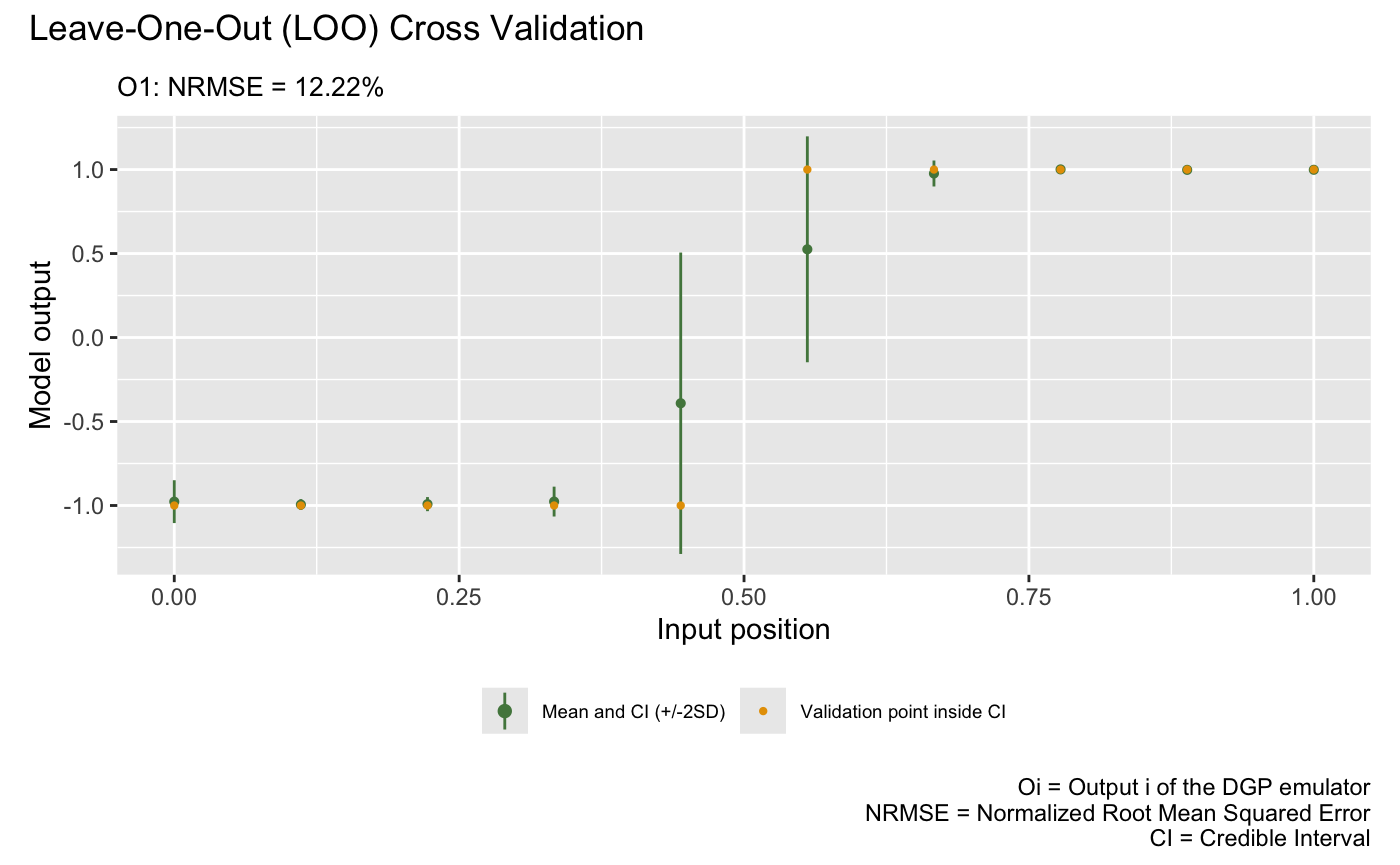
The second validation plot is the Out-Of-Sample (OOS) validation plot that requires an out-of-sample testing data set. Here we generate an OOS data set that contains 10 testing data points:
We can now perform OOS validation:
plot(m,oos_x,oos_y)## Validating and computing ... done
## Post-processing OOS results ... done
## Plotting ... done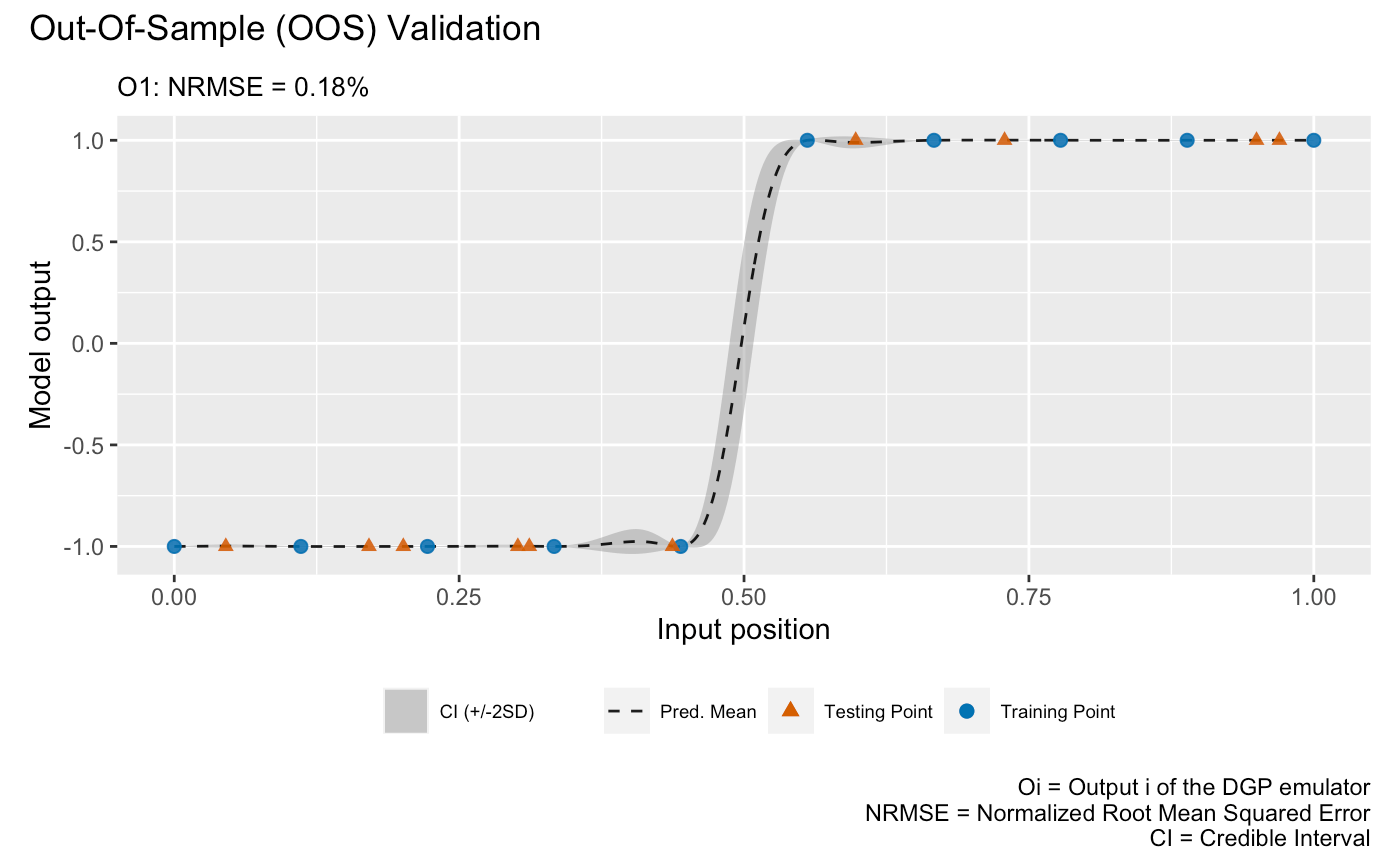
Note that the style argument to the plot()
function can be used to draw different types of plot (see
?plot).
Prediction
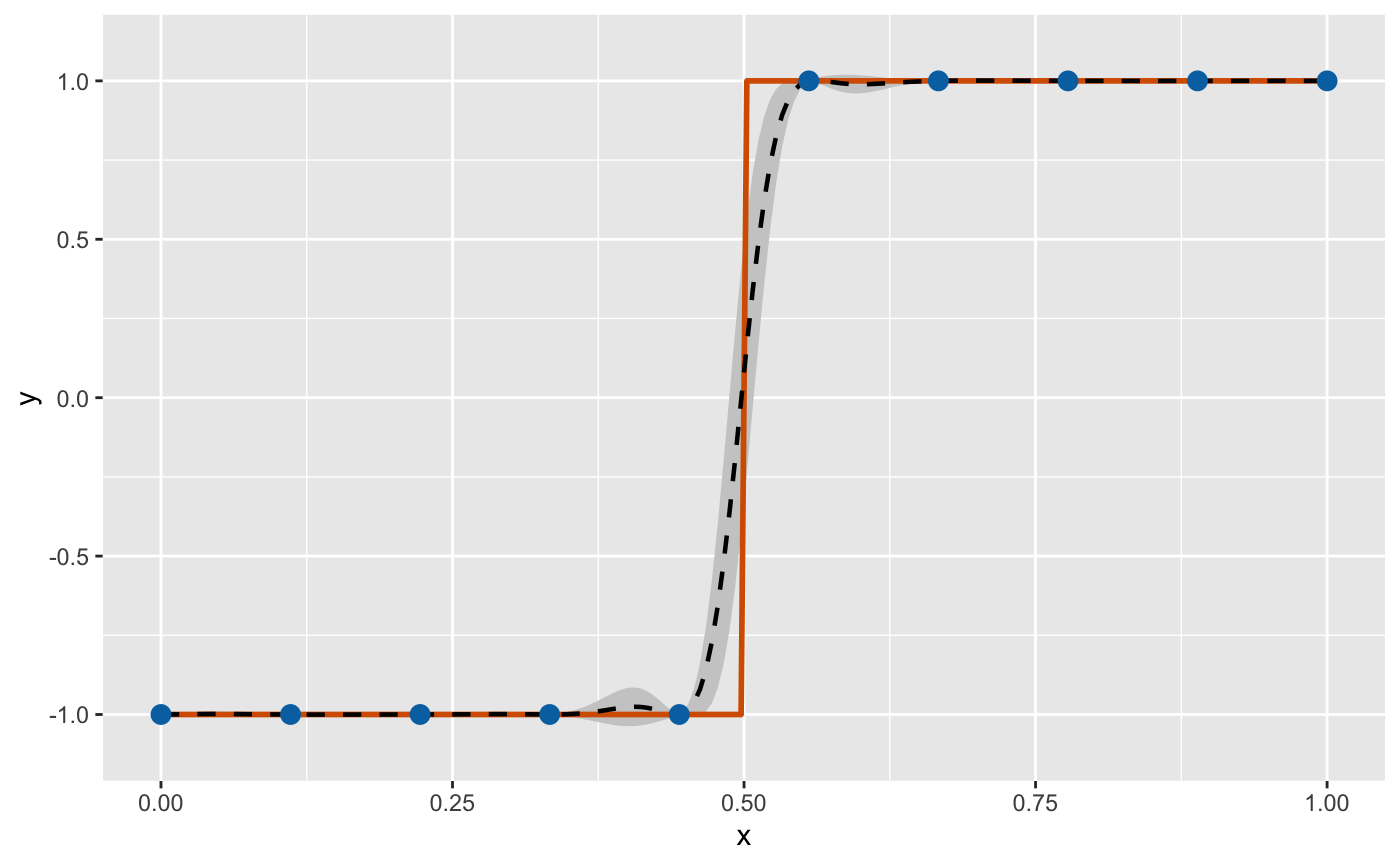
Once the validation is done, we can make predictions from the DGP emulator. We generate 200 data points from the step function over :
and predict at these locations:
m <- predict(m, x = test_x)The predict() function returns an updated DGP emulator
m that contains a slot named results that
gives the posterior predictive means and variances at testing positions.
We can extract this information and plot the emulation results to check
the predictive performance of our constructed DGP emulator:
mu <- m$results$mean # extract the predictive means
sd <- sqrt(m$results$var) # extract the predictive variance and compute the predictive standard deviations
# compute predictive bounds which are two predictive standard deviations above and below the predictive means
up <- mu + 2*sd
lo <- mu - 2*sd
ggplot() +
# credible interval
geom_ribbon(data = data.frame(x = test_x, ymin = lo, ymax = up),
aes(x = x, ymin = ymin, ymax = ymax), fill = "grey80") +
# underlying truth
geom_line(data = data.frame(x = test_x, y = test_y),
aes(x = x, y = y), colour = "#D55E00", linewidth = 1) +
# predictive mean
geom_line(data = data.frame(x = test_x, y = mu),
aes(x = x, y = y), colour = "black", linetype = "dashed", linewidth = 0.8) +
# training points
geom_point(data = data.frame(x = X, y = Y),
aes(x = x, y = y), colour = "#0072B2", size = 3) +
coord_cartesian(ylim = c(-1.1, 1.1)) +
labs(x = "x", y = "y")